Convergence de Série harmonique alternée

On considère la suite définie par la somme .

1. En calculant les premiers termes de cette suite, montrer qu'elle n'est pas monotone.
2. On pose et 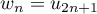, Montrer que ces suites sont adjacentes. Que peut-on en conclure ?

Correction