Droites coplanaires, sécantes, …
Soit  un réel. On considère les droites
un réel. On considère les droites
 et
et
 .
.
-
 et
et 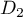 sont-elles parallèles?
sont-elles parallèles?
- Déterminer
 pour qu'elles soient coplanaires.
pour qu'elles soient coplanaires.
Donner alors les coordonnées du point d'intersection de et
et  et une équation du plan contenant
et une équation du plan contenant  et
et  .
.
Correction
Soit un réel. On considère les droites
un réel. On considère les droites
 et
et
 .
.
Cacher la correction
Soit
-
 et
et  sont deux vecteurs orthogonaux
de
sont deux vecteurs orthogonaux
de  dont un vecteur directeur est donc
dont un vecteur directeur est donc
 .
.
De même pour dirigée par
dirigée par
 .
.
Comme et
et  ne sont pas colinéaires,
ne sont pas colinéaires,
 et
et  ne sont pas parallèles.
ne sont pas parallèles.
- Ces droites sont donc coplanaires si et seulement si elles
sont sécantes. Soit
 l'éventuel point d'intersection,
alors
l'éventuel point d'intersection,
alors
 .
.
En soutrayant la 1ère équation à la 3ème, on obtient ,
et alors la 2ème fournit
,
et alors la 2ème fournit  , puis la 1ère
, puis la 1ère  .
Enfin, la dernière donne alors que les droites sont sécantes
en
.
Enfin, la dernière donne alors que les droites sont sécantes
en  si et seulement si
si et seulement si  .
.
Un vecteur normal au plan contenant et
et  est donné par
est donné par
 ,
donc
,
donc  , et comme
, et comme  ,
on obtient
,
on obtient  d'où
d'où
![\[P:-4x-y-6z-1=0\iff 4x+y+6z+1=0\]](/Generateur-Devoirs/Colles/Geom3D/ex7_c/27.png)
Cacher la correction
Tag:Géométrie dans l'espace
Autres sujets au hasard:
