Équation de cercle dans l'espace
À tout réel  , on associe le point
, on associe le point  de coordonnées
de coordonnées
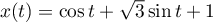 ,
,
 et
et
 .
.
- Calculer
 .
.
- Calculer
 .
.
- En déduire que
 est toujours élément d'un cercle
dont on précisera le centre et le rayon.
est toujours élément d'un cercle
dont on précisera le centre et le rayon.
Correction
Cacher la correction
-
 et donc
et donc  ,
avec
,
avec  le plan d'équation
le plan d'équation  .
.
-
 et donc
et donc  ,
avec
,
avec  la sphère d'équation
la sphère d'équation  .
.
-
 .
Le centre de ce cercle est le projeté orthogonal de
.
Le centre de ce cercle est le projeté orthogonal de  ,
centre de la sphère, sur le plan
,
centre de la sphère, sur le plan  .
On cherche donc
.
On cherche donc  tel que le vecteur
tel que le vecteur  est colinéaire à
est colinéaire à  (vecteur normal du plan).
On trouve A(1,1,1).
(vecteur normal du plan).
On trouve A(1,1,1).
Le rayon du cercle est, par exemple
du cercle est, par exemple  .
.
Cacher la correction
Tag:Géométrie dans l'espace
Autres sujets au hasard:
