Équation différentielle - 2nd ordre, coefficients constants
Résoudre: 
Correction
L'équation homogène associée a pour équation caractéristique
a pour équation caractéristique  de racines
de racines 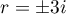 , et donc pour
solution
, et donc pour
solution  ,
,  .
.
On peut rechercher une solution particulière sour la forme ,
pour laquelle
,
pour laquelle
 .
On obtient ainsi une solution particulière en choisissant
.
On obtient ainsi une solution particulière en choisissant
 .
.
Les solutions de l'équation sont donc les fonctions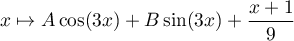 .
.
Cacher la correction
L'équation homogène associée
On peut rechercher une solution particulière sour la forme
Les solutions de l'équation sont donc les fonctions
Cacher la correction
Tag:Équation différentielle
Autres sujets au hasard:
