Équations paramétriques de droites et intersection
Dans un repère  du plan,
on considère le point
du plan,
on considère le point 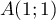 , le vecteur
, le vecteur
 et la
droite
et la
droite  dont une équation cartésienne
est
dont une équation cartésienne
est  .
.
Correction
Cacher la correction
-

-
 est un vecteur directeur de
est un vecteur directeur de  qui est colinéaire à
qui est colinéaire à  donc les droites sont parallèles.
donc les droites sont parallèles.
Comme les droites sont prallèles et distinctes,
et donc
les droites sont prallèles et distinctes,
et donc  .
.
Cacher la correction
Tag:Géométrie plane cartésienne
Autres sujets au hasard:
