Estimation pour le lancer de dé
On jette 3600 fois un dé équilibré. Minorer la probabilité que le nombre d'apparitions du numéro 1 soit compris entre 500 et 700.
Correction
Soit
la variable aléatoire égale au nombre d'apparitions du chiffre 1
au cours de ces lancers.
suit une loi binomiale de paramètres 3600 et 1/6,
et donc 
et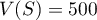 
.
On a de plus
![\[500\leqslant S\leqslant700\iff |S-E(S)|\leqslant100\]](/Generateur-Devoirs/Colles/VAIE/Estim-de_c/5.png)
puis, par l'inégalité de Bienaymé-Tchebichev,
![\[P\Bigl(|S-E(S)\geqslant120\Bigr)\leqslant\dfrac{500}{100^2}\leq 0,05\]](/Generateur-Devoirs/Colles/VAIE/Estim-de_c/6.png)
On en déduit que
![\[P(500\leqslant S\leqslant700)\geqslant 1-0,05=0,95\]](/Generateur-Devoirs/Colles/VAIE/Estim-de_c/7.png)
En particulier, la probabilité que le numéro 1 apparaisse entre 500 et 700 fois au cours de ces
lancers est supérieur à 0,95.
Cacher la correction
Soit
la variable aléatoire égale au nombre d'apparitions du chiffre 1
au cours de ces lancers.
suit une loi binomiale de paramètres 3600 et 1/6,
et donc et .
On a de plus
puis, par l'inégalité de Bienaymé-Tchebichev,
On en déduit que
En particulier, la probabilité que le numéro 1 apparaisse entre 500 et 700 fois au cours de ces
lancers est supérieur à 0,95.
Cacher la correction
Tag:VA: inégalités & estimation
Autres sujets au hasard:
