Famille construite à partir de n vecteurs libres


Soit $(v_1,\dots,v_n)$ une famille libre d'un $\mathbb R$-espace vectoriel $E$. Pour $k=1,\dots,n$, on pose $w_k=v_k+v_{k+1}$ et $w_n=v_n+v_1$.
Etudier l'indépendance linéaire de la famille $(w_1,\dots,w_n)$.

Correction
Soit $\lambda_1,\dots,\lambda_n$ tels que
\[\lambda_1w_1+\dots +\lambda_nw_n=0\]

alors,
\[\sum_{k=1}^{n-1}\lambda_k(v_k+v_{k+1})+\lambda_n (v_n+v_1)=0\]

ou encore
\[(\lambda_1+\lambda_n)v_1+\sum_{k=2}^n(\lambda_k+\lambda_{k+1})v_k=0.\]

Comme le système $(v_1,\dots,v_n)$ est linéairement indépendant, on en déduit le système :
\[\la\begin{array}{rcl} \lambda_n&=&-\lambda_1\\ \lambda_k&=&-\lambda_{k-1}\textrm{ pour }2\leq k\leq n. \enar\right.\]

La deuxième égalité donne facilement par récurrence, pour $2\leq k\leq n$, $\lambda_k=(-1)^{k-1}\lambda_1$. En particulier, on a $\lambda_n=(-1)^{n-1}\lambda_1$. On discute maintenant suivant la parité de $n$ :
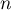  • Si $n$ est impair, alors on a à la fois $\lambda_n=\lambda_1$ et $\lambda_n=-\lambda_1$. Ceci impose $\lambda_1=0$, et par suite $\lambda_k=0$ pour tout $k$. Le système est libre.
  • Si $n$ est pair, la dernière équation est $\lambda_n=-\lambda_1$, qui est la même que la première.
    On a alors un système de $n-1$ équations à $n$ inconnues. Si on fixe par exemple $\lambda_1=1$, on a $\lambda_k=(-1)^k$, et on a donc trouvé une combinaison linéaire nulle non triviale $\lambda_1w_1+\dots+\lambda_nw_n=0$.
    La famille est liée.


Cacher la correction


Tag:Espace vectoriel

Autres sujets au hasard: Lancer de dés
LongPage: h2: 0 - h3: 0