Fonction avec sinus et cosinus hyperbolique


Étudier les variations de la fonction $f:x\mapsto2\cosh^2x-\sinh2x$.

Correction
On a $f(x)=2u^2(x)-v(2x)$, avec $u(x)=\cosh(x)$ donc $u'(x)=\sinh(x)$, et $v(x)=\sinh(x)$ donc $v'(x)=\cosh(x)$.
Ainsi $f'(x)=2\tm2u'(x)\,u(x)-2v'(2x) =4\sinh(x)\cosh(x)-2\cosh(2x)$
En revenant à l'écriture exponentielle, cette expression s'écrit aussi,
\[\begin{array}{ll} f'(x) &=4\tm\dfrac{e^x-e^{-x}}{2}\tm\dfrac{e^x+e^{-x}}{2} -2\tm\dfrac{e^{2x}+e^{-2x}}{2}\\[1em] &=\left( e^x-e^{-x}\rp\tm\left( e^x+e^{-x}\rp -\left( e^{2x}+e^{-2x}\rp\\[1em] &=\left( e^{2x}-e^{-2x}\right) -\left( e^{2x}+e^{-2x}\rp\\[1em] &=-2e^{-2x} \enar\]


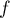Ainsi, pour tout réel $x$, $f'(x)<0$ et donc $f$ est strictement décroissante sur $\R$.

Remarque: On remarque de plus que $f'=g'$ avec $g(x)=e^{-2x}$, et donc $f=g+k$, pour une certaine constante $k\in\R$.
Enfin, comme $f(0)=2$ et $g(0)=1$, on en déduit que $k=1$, soit que $f(x)=e^{-2x}+1$, pour tout réel $x$.

Remarque, suite:
\[\begin{array}{ll} f(x) &=2\cosh^2x-\sinh2x\\ &=2\lp\dfrac{e^x+e^{-x}}{2}\rp^2-\dfrac{e^{2x}-e^{-2x}}{2}\\[1em] &=\dfrac{e^{2x}+e^{-2x}+2e^{x}e^{-x}}{2}-\dfrac{e^{2x}-e^{-2x}}{2}\\[1em] \enar\]


Enfin, comme $e^{x}e^{-x}=e^0=1$, on trouve finalement, qu'on aurait pu trouver dès le début que $f(x)=e^{-2x}+1$ pour tout réel $x$, ce qui aurait faciliter (grandement) l'exercice…

Cacher la correction


Tag:Dérivée

Autres sujets au hasard: Lancer de dés
LongPage: h2: 0 - h3: 0