Fonction composée avec arctan


Étudier la fonction $f$ définie par l'expression $f(x)=\arctan\dfrac{2(1-x)}{2x-x^2}$.
Exprimer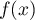 $f(x)$ en fonction de $\arctan(x-1)$ sur $]0;2[$.

Correction
$f(x)=\arctan\dfrac{2(1-x)}{2x-x^2}$.
$\arctan$ est définie sur $\R$, donc $f$ est définie sur $D_f=\R\setminus\la0;2\ra$.
On a $f=\arctan(u)$, avec $u=\dfrac{v}{w}$, donc $f'=u'\tm\dfrac{1}{1+u^2}$, soit, pour tout $x\in D$,
\[\begin{array}{ll} f'(x)&=\dfrac{-2(2x-x^2)-2(1-x)(2-2x)}{(2x-x^2)^2} \tm\dfrac{1}{1+\lp\dfrac{2(1-x)}{2x-x^2}\rp^2}\\ &=\dfrac{-2x^2+4x-4}{(2x-x^2)^2} \tm\dfrac{{(2x-x^2)^2}}{(2x-x^2)^2+4(1-x)^2}\\ &=-2\dfrac{x^2-2x+2}{(2x-x^2)^2+4(1-x)^2} \enar\]

Comme pour tout $x$ réel, $x^2-2x+2>0$ (le discriminant du trinôme est $\Delta=-4<0$), et que le dénominateur est unes somme de deux carrés donc positif aussi, on en déduit que $f'(x)<0$ et donc que $f$ est décroissante sur $D_f$.


D'autre part, si $g(x)=\arctan(x-1)$, alors $g'(x)=\dfrac{1}{(x-1)^2+1}=\dfrac{1}{x^2-2x+2}$
On peur alors remarquer que $(2x-x^2)^2+4(1-x)^2=x^4-4x^3+8x^2-8x+4=\left( x^2-2x+2\rp^2$, et donc que $f'(x)=-2\dfrac{x^2-2x+2}{\left( x^2-2x+2\rp^2}=-2\dfrac{1}{x^2-2x+2}=-2g'(x)$.
Ainsi, $f=-2g+C$, $C\in\R$.
Sur $]0;2[$, $f(1)=\arctan(0)=0=-2g(0)+C=C$, et donc $f(x)=-2\arctan(x-1)$.

Cacher la correction


Tag:Dérivée

Autres sujets au hasard: Lancer de dés
LongPage: h2: 0 - h3: 0