Intersection de courbes: cercle et droite
Déterminer l'intersection des courbes
et 
.
et .
Correction
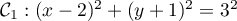est le cercle de rayon 
et de centre 
.
On cherche donc l'intersection de ce cercle et de la droite
.
![\[\begin{array}{ll}
M(x;y)\in\mathcal{C}_1\cap\mathcal{C}_2
&\iff
\la\begin{array}{ll}
x^2+y^2-4x+2y-4=0\\
x+3y-2=0
\enar\right. \\[1.2em]
&\iff
\la\begin{array}{ll}
(-3y+2)^2+y^2-4(-3y+2)+2y-4=10y^2+2y-8=0\\
x=-3y+2
\enar\right.\\
\enar\]](/Generateur-Devoirs/Colles/Geom2D/ex2_c/5.png)
On trouve donc 2 points d'intersection
et alors 
,
et 
et 
.
Cacher la correction
est le cercle de rayon
et de centre .
On cherche donc l'intersection de ce cercle et de la droite
.On trouve donc 2 points d'intersection
et alors ,
et et .
Cacher la correction
Tag:Géométrie plane cartésienne
Autres sujets au hasard:
