Logarithme, encadrements et convergence d'une somme


  1. Montrer que pour tout $u>-1$, $\ln(1+u)\leqslant u$.
    En déduire que, pour $x>1$, $\ln\dfrac{x+1}x\leqslant\dfrac1x\leqslant\ln\dfrac{x}{x-1}$.
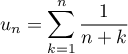  2. Quelle est la nature de la suite définie par $u_n=\dsp\sum_{k=1}^n\dfrac1{n+k}$ ?

Correction
  1. Il suffit d'étudier la fonction $f:u\mapsto\ln(1+u)-u$, qui est bien définie est dérivable sur $]-1;+\infty[$, et pour laquelle $f'(u)=\dfrac1{1+u}-1=-\dfrac{u}{1+u}$. Le tableau de variation de $f$ montre alors un maximum en $u=1$ et qui vaut $f(1)=0$.
    Ainsi, pour $u>-1$, on a $f(u)<0\iff\ln(1+u)<u$.

    On va utiliser deux fois ce résultat.
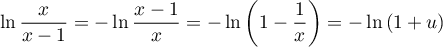    Avec $u=\dfrac1x$, on a donc d'une part $\ln(1+u)=\ln\lp1+\dfrac1x\rp=\ln\dfrac{x+1}x\leqslant u=\dfrac1x$, et d'autre part avec $u=-\dfrac1x>-1$ $\ln\dfrac{x}{x-1}=-\ln\dfrac{x-1}x=-\ln\lp1-\dfrac1x\rp=-\ln\lp1+u\rp$ On a donc $\ln(1+u)<u\iff\ln\lp1-\dfrac1x\rp<-\dfrac1x$ d'où l'inégalité de droite recherchée.
  2. On utilise l'encadrement précédent, avec $x=n+k$,
    \[\ln\dfrac{n+k+1}{n+k}\leqslant\dfrac1{n+1}\leqslant\ln\dfrac{n+k}{n+k-1}\]

    On somme ensuite ces inégalités. Le terme de gauche est télescopique:
    \[\sum_{k=1}^n\ln\dfrac{n+k+1}{n+k} =\sum_{k=1}^n\ln(n+k+1)-\ln(n+k) =\ln(2n+1)-\ln(n+1) =\ln\dfrac{2n+1}{n+1}\]


    De même, pour le terme de gauche, on obtient
    \[\sum_{k=1}^n\ln\dfrac{n+k}{n+k-1}=\ln\dfrac{2n}n=\ln2\]

    On a ainsi obetnu l'encadrement
    \[\ln\dfrac{2n+1}{n+1}\leqslant\sum_{k=1}^n\dfrac1{n+k}\leqslant\ln2\]

    Maintenant, comme $\ln\dfrac{2n+1}{n+1}\longrightarrow\ln2$, on a, grâce au théorème des gendarmes, que $u_n=\dsp\sum_{k=1}^n\dfrac1{n+k}\longrightarrow2$.


Cacher la correction


Tag:Sommes

Autres sujets au hasard: Lancer de dés
LongPage: h2: 0 - h3: 0