Nombre de racines de la dérivée d'un polynôme

Soit la fonction définie sur par .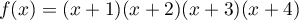
Démontrer que l'équation admet exactement trois solutions réelles distinctes.

Correction
admet 4 racines évidentes: .
Ainsi, d'après le théorème de Rolle, appliqué trois fois respectivement sur , et , on obtient trois racines de , distinctes car elles appartiennent à des intervalles disjoints , et .

Enfin, comme est un polynôme de degré 4, est un polynôme de degré 3. Ainsi admet au plus trois racines.
D'après ce qui précède, admet donc exactement trois racines réelles.

Cacher la correction