Rayon de convergence


Déterminer le rayon de convergence de la série entière $\dsp\sum_n a^{\sqrt{n}}z^n,\ a>0$

Correction
Pour $a=0$ le terme général est nul et la série converge trivialement pour tout $z$.

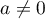Pour $a\not=0$, on applique la règle de d'Alembert à $u_n=a^{\sqrt{n}}|z|^n$:
\[\frac{u_{n+1}}{u_n}=|z|a^{\sqrt{n+1}-\sqrt{n}}\]

Or,
\[\begin{array}{ll}\sqrt{n+1}-\sqrt{n}&=\sqrt{n}\big((1+1/n)^{1/2}-1)\\[.7em] &=\sqrt{n}\left(1+\frac{1}{2n}-1+o\left(\frac1n\right)\right)\to 0\enar\]

Ainsi, on obtient que
\[\frac{u_{n+1}}{u_n}\to |z|a^0=|z|\]

et on en déduit que la série converge absolument pour $|z|<1$ et diverge pour $|z|>1$.
Le rayon de convergence de la série entière est donc 1.

Cacher la correction


Tag:Séries entières

Autres sujets au hasard: Lancer de dés
LongPage: h2: 0 - h3: 0