Recherche de fonctions avec une propriété intégrale
Soit ![$f:[a;b]\to\R$](/Generateur-Devoirs/Colles/Integrale/exR1/1.png) continue et telle que
continue et telle que
 .
.
On sait de plus que .
Que dire de
.
Que dire de  ?
?
On sait de plus que
 .
Que dire de
.
Que dire de Correction
On remarque que ,
ou encore, par soustraction et linéarité,
,
ou encore, par soustraction et linéarité,
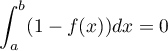 .
.
Comme pour tout![$x\in[a;b]$](/Generateur-Devoirs/Colles/Integrale/exR1_c/3.png) ,
,
 , on a pour tout
, on a pour tout ![$x\in[a;b]$](/Generateur-Devoirs/Colles/Integrale/exR1_c/5.png) ,
,  avec
avec  continue sur
continue sur ![$[a;b]$](/Generateur-Devoirs/Colles/Integrale/exR1_c/8.png) ;
on a donc nécessairement
;
on a donc nécessairement  ou encore
ou encore  .
.
Remarque, ou autre méthode: on peut réécrire dès le début
![\[\dsp\dfrac1{b-a}\int_a^bf(x)dx=1\]](/Generateur-Devoirs/Colles/Integrale/exR1_c/11.png)
c'est-à-dire que la valeur moyenne de est 1.
Or
est 1.
Or  est continue et toujours inférieure ou égale à 1, donc nécessairement
est continue et toujours inférieure ou égale à 1, donc nécessairement  pour tout
pour tout ![$x\in[a;b]$](/Generateur-Devoirs/Colles/Integrale/exR1_c/15.png) .
.
La démonstration rigoureuse est alors celle donnée précedemment.
Cacher la correction
On remarque que
 ,
ou encore, par soustraction et linéarité,
,
ou encore, par soustraction et linéarité,
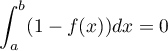 .
.
Comme pour tout
Remarque, ou autre méthode: on peut réécrire dès le début
![\[\dsp\dfrac1{b-a}\int_a^bf(x)dx=1\]](/Generateur-Devoirs/Colles/Integrale/exR1_c/11.png)
c'est-à-dire que la valeur moyenne de
La démonstration rigoureuse est alors celle donnée précedemment.
Cacher la correction
Tag:Intégrale
Autres sujets au hasard:
