Suite implicite définie par une intégrale impropre
Soit  définie par:
définie par:
![\[H(x)=\int_x^{+\infty}\dfrac{e^{-t^2}}{2(1+t)}dt\]](/Generateur-Devoirs/Colles/Integrale/IISI/2.png)
et la suite définie par
la suite définie par  et
et
 .
.
Correction
![\[H(x)=\int_x^{+\infty}\dfrac{e^{-t^2}}{2(1+t)}dt\]](/Generateur-Devoirs/Colles/Integrale/IISI/2.png)
et
- Déterminer les valeurs de
 pour lesquelles
pour lesquelles  est convergente.
est convergente.
- Étudier les variations de
 sur
sur ![$]0;+\infty[$](/Generateur-Devoirs/Colles/Integrale/IISI/9.png) . Préciser la limite en
. Préciser la limite en  .
.
- Prouver que
 pour tour entier
pour tour entier  .
.
- Montrer qu'il existe un unique
 tel que
tel que  .
.
- Montrer que, pour tout entier
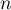 ,
,
 .
.
- En déduire que
 converge.
converge.
Correction
Tags:IntégraleSuites
Autres sujets au hasard:
