Quadratic and polynomial forms

Français

Solving quadratic and polynomial equations and inequalities


Contents

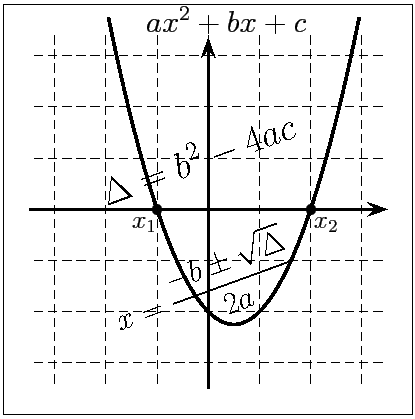
$\displaystyle \begin{pspicture}(-4,0)(4,4)\psset{unit=1cm,arrowsize=8pt}\ps... ...t(2.3,-0.3){\large$x_2$}%\rput(0.35,3.7){\Large$ax^2+bx+c$}\end{pspicture}$

Quadratic form



Solving quadratic equations


Definition A quadratic expression is an expression which can be written as $ ax^2+bx+c$ , where $ a$, $ b$ et $ c$ represent numbers such that $ a\not=0$.
A number $ x$ solution of the quadratic equation $ ax^2+bx+c=0$ is also called a root of the quadratic expression $ ax^2+bx+c$.

Example: Some quadratic expressions and their coefficients

Quadratic expressions $ a$ $ b$ $ c$
$ P(x)=3x^2+2x-5$ $ a=3$ $ b=2$ $ c=-5$
$ Q(x)=\sqrt{2}x^2-3x+\dfrac23$ $ a=\sqrt{2}$ $ b=-3$ $ c=\dfrac23$
$ R(x)=-x^2+\dfrac52x$ $ a=-1$ $ b=\dfrac52$ $ c=0$
$ S(x)=3x^2-\left(1-\sqrt{2}\right)x-\pi$ $ a=3$ $ b=-\left(1-\sqrt{2}\right)$ $ c=-\pi$
$ T(x)=\dfrac65 x^2-3$ $ a=\dfrac65$ $ b=0$ $ c=-3$
$ U(x)=(x-2)^2+3(x+3)$ $ a=\dots$ $ b=\dots$ $ c=\dots$


Definition The number $\displaystyle \Delta=b^2-4ac .$ is called the discriminant of the quadratic expression   $ ax^2+bx+c$

Example: Some quadratic expressions and their discriminant

Quadratic expressions $ a$ $ b$ $ c$ $ \Delta$
$ P(x)=3x^2+2x-5$ $ a=3$ $ b=2$ $ c=-5$ $ \Delta=64$
$ Q(x)=x^2+2x+1$ $ a=1$ $ b=2$ $ c=1$ $ \Delta=0$
$ R(x)=x^2-\sqrt{2}x-5$ $ a=1$ $ b=\sqrt{2}$ $ c=-5$ $ \Delta=22$


Theorem
$ \bullet$ If $ \Delta>0$, the quadratic equation $ ax^2+bx+c=0$ (where $ a\not=0$) has two distinct solutions (also called roots):
$\displaystyle x_1=\dfrac{-b-\sqrt{\Delta}}{2a}$    et $\displaystyle \quad x_2=\dfrac{-b+\sqrt{\Delta}}{2a}$
$ \bullet$ If $ \Delta=0$, the quadratic equation $ ax^2+bx+c=0$ (where $ a\not=0$ ) has a unique solution (or root): $\displaystyle x_0=\dfrac{-b}{2a}$
$ \bullet$ If $ \Delta<0$, the quadratic equation $ ax^2+bx+c=0$ has no real solution.


Exercice 1. Solve the following quadratic equations

a) $ x^2-2x+1=0$


b) $ x^2-1=0$

c) $ 4x^2+8x-5=0$

d) $ 3x^2+x+6=0$


Sign of a quadratic expression


Theorem Let $ f(x)=ax^2+bx+c$, ( where $ a\not=0$), then:
$ \bullet$ if $ \Delta>0$, the equation $ f(x)=0$ has two solutions $ x_1$ and $ x_2$ and
$\displaystyle \begin{tabular}{\vert c\vert ccccccc\vert}\hline $x$ & $-\infty... ... & Signe de & \\&& de $a$ && de $-a$ && de $a$& \hline\end{tabular} $


$ \bullet$ if $ \Delta=0$, the equation $ f(x)=0$ has a unique solution $ x_0$ and
$\displaystyle \begin{tabular}{\vert c\vert ccccc\vert}\hline $x$ & $-\infty$\... ...ut(0,-0.2){$0$}& Signe &\\&& de $a$ && de $a$& \hline\end{tabular} $


$ \bullet$ if $ \Delta<0$, the quadratic expression $ f(x)$ has no root and
$\displaystyle \begin{tabular}{\vert c\vert ccc\vert}\hline $x$ & $-\infty$ && $+\infty$ \hline $f(x)$ && Signe de $a$ & \hline \end{tabular} $


Exercice 2. Give the sign of the following quadratic functions:

a) $ P(x)=x^2-2x+1$

b) $ Q(x)=x^2-1$

c) $ S(x)=-3x^2+5x-2$

d) $ T(x)=2x^2+x+3$

Exercices


Exercice 3. Solve the following inequalities:

a) $ x^2-2x+1>0$


b) $ -3x^2+5x-2\leqslant 0$


c) $ x(2x-5)\geqslant x-6$



Exercice 4. Give the sign of the following expression:
a) $ f(x)=-x^2+x-3$



b) $ g(x)=x-\dfrac{1}{x}$



c) $ h(x)=2x+\dfrac{4}{x-3}$



Exercice 5. (Examples of equations reducible to quadratic form)
By first defining $ X=x^2$ , solve the following equations:

a) $ x^4-13x^2+36=0$



b) $ x^2+\dfrac{1}{x^2}-6=0$




Exercice 6. Determine the intersection points (if they exist) between the parabola $ \mathcal{P}$ and the line $ \mathcal{D}$ which equations are: $ \mathcal{P}: y=x^2-3x+1$     et     $ \mathcal{D}: y=-2x+1$



Exercice 7. Determine the intersection points (if they exist) between the two parabolas $ \mathcal{P}$ and $ \mathcal{P}'$ where: $ \mathcal{P}: y=x^2-x+2$     et     $ \mathcal{P}': y=-x^2+2x-6$



Exercice 8. (A parametric quadratic equation)
Let $ m$ be a real number. We consider the quadratic equation    $ 4x^2+(m-1)x+1=0$.
Determine the values of $ m$ for which this equation has a unique solution.
Give then this solution.




Polynomial expressions



Fundamental theorem


Definition
A polynomial is an expression which can be written in the form
$\displaystyle ax^n+bx^{n-1}+cx^{n-2}+\dots+dx+e$
where $ a$, $ b$, $ c$, $ d$ and $ e$ are real numbers, and $ n$ is a positive integer.
The integer $ n$ is the degree of the polynomial.


Examples:
$ \bullet$ $ P(x)=3x^4-2x^3+\dfrac12 x^2-\sqrt{2}x+3$ is a polynomial of degree 4.
$ \bullet$ $ Q(x)=5x^7-3x^2+4$ is a polynomial of degree 7.
$ \bullet$ $ R(x)=x^2+x+1$ is a polynomial of degree 2. This is also a quadratic expression: actually all quadratic expression are second degree polynomial.

Factor Theorem (Fundamental property for polynomials)
Let $ P(x)$ be a polynomial of degree $ n$ and $ a$ a root of $ P$ (that is $ P(a)=0$).
Then, $ P(x)$ can be factored by $ (x-a)$: there exists a polynomial $ Q(x)$ of degree $ n-1$ such that
$\displaystyle P(x)=(x-a)Q(x)$


Exercice 9. We consider the polynomial function $ P(x)=x^3-x^2-x-2$.
  1. Show that $ 2$ is a root of $ P$, then give a factorization of $ P$.

  2. Déterminer alors toutes les solutions de l'équation $ P(x)=0$.



corollary
If the quadratic expression $ ax^2+bx+c$ has two roots $ x_1$ and $ x_2$, then it can be factored as $ ax^2+bx+c=a(x-x_1)(x-x_2)$.


Exercice 10. Give a factored expression for the following quadratic expressions.
  1. $ P(x)=x^2-3x+2$

  2. $ Q(x)=2x^2+2x-4$



Exercices



Exercice 11. Let the third degree polynomial $ P(x)=2x^3+7x^2+7x+2$.
  1. Show that $ -2$ is a root of $ P$, then give a factored form of $ P$.

  2. Solve the equation $ P(x)=0$, and then give the sign of the expression   $ P(x)$.



Exercice 12. Beam deflection
A 2 meter length beam is based on three simple supports $ A$, $ B$ and $ C$, supporting point $ B$ being located in the middle of the segment $ [AC]$.
The beams supports a uniformly distributed load of 1000 N.m$ ^{-1}$ (newtons metre). Under the action of this charge, the beam deforms.

$\displaystyle %\fbox{\begin{pspicture}(0,0)(11,2.2)\psset{unit=1cm}\pspolyg... ...\rput(4.5,-0.8){$x_m$}\psline[linestyle=dashed](8,-1)(8,-0.2)\end{pspicture}$


One can show that the point located between $ B$ and $ C$ where the deformation is maximum, is such that $ x_m$ is a solution of the equation:
$\displaystyle 32x^3-156x^2+240x-116=0 .$

  1. Verify that $ 1$ is a solution of this equation.

  2. Give a factored form of the polynomial expression of this equation and then solve it.

  3. Find $ x_m$, the location between points $ B$ and $ C$, where the beam is at most deformed.


Some more exercices on quadratic forms ? Lien vers les devoirs corrigés