Solving equations
"A demonstration is not anything other than the resolution of a truth in other truths already known."
Gottfried Wilhelm Leibniz (1646 - 1716)
German mathematician, philosopher, scientist, diplomat, librarian and lawyer
German mathematician, philosopher, scientist, diplomat, librarian and lawyer
Solving an equation, for example
 where
where  is an algebraic expression containing the unknown
is an algebraic expression containing the unknown
 ,
is to find all solutions
of the equation, that is to find
all the values of the number
,
is to find all solutions
of the equation, that is to find
all the values of the number  such that equality
such that equality  is true.
is true.
 where
where  is an algebraic expression containing the unknown
is an algebraic expression containing the unknown
 ,
is to find all solutions
of the equation, that is to find
all the values of the number
,
is to find all solutions
of the equation, that is to find
all the values of the number  such that equality
such that equality  is true.
is true.
Example:
For the equation  ,
We can verify that
,
We can verify that  is a solution.
is a solution.
Indeed, if we replace by
by
 ,
we actually get
,
we actually get
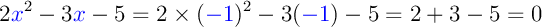
Thus, is a solution of this equation.
Nevertheless, can not claim to have solved it because we do not know a priori if there are others.
is a solution of this equation.
Nevertheless, can not claim to have solved it because we do not know a priori if there are others.
We do not know all solutions.
We could also check that is an other solution:
is an other solution:

So we know a second solution, but again we can not yet claim to have solved the equation ...
 ,
We can verify that
,
We can verify that  is a solution.
is a solution.
Indeed, if we replace
 by
by
 ,
we actually get
,
we actually get
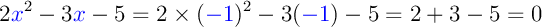
Thus,
 is a solution of this equation.
Nevertheless, can not claim to have solved it because we do not know a priori if there are others.
is a solution of this equation.
Nevertheless, can not claim to have solved it because we do not know a priori if there are others.
We do not know all solutions.
We could also check that
 is an other solution:
is an other solution:

So we know a second solution, but again we can not yet claim to have solved the equation ...
The purpose of what follows is just solving equations, that is to say,
the determination of all solutions of an equation (to find them, and
be sure to get all of them).
One can solve only five types of equation. All other equations (second or higher degree equations, trigonometric equations, logarithmic, ...), are then based on these five types.
One can solve only five types of equation. All other equations (second or higher degree equations, trigonometric equations, logarithmic, ...), are then based on these five types.
-
Linear equations (first degree equations):

solved according to: .
.
-
Zero factor equations:

solved using the "zero factor property" (or "Rule" or "Principle"): if a product of two terms is zero then at least one of the terms has to be zero

Note 1: Of course, there may be more than two factors, eg for three factors:

Note 2: These equations are fundamental. They allow to decompose, equivalently, an equation into several simpler equations.
An equation may not directly and apparently be displayed as products of factors; it is often possible to transform to get a factored expression.
For this particular reason, factorization is a fundamental operation in mathematics.
-
Zero quotient equations:

which are very similar to zero factor equations, except that here the denominator can not be zero:

Note: Values of for which denominateur is zero:
for which denominateur is zero:
 ,
quite apart from any equation, are such that the quotient
,
quite apart from any equation, are such that the quotient
 does not exist
(division by
does not exist
(division by
 does not exists !!).
does not exists !!).
These values of ar prohibited values
for the expression
ar prohibited values
for the expression
 and cannot, in any way, be solutions.
and cannot, in any way, be solutions.
-
(Perfect) square equations:

for which, depending on the sign of the real number :
:
- if
 :
then equation
:
then equation  has no solution;
has no solution;
(because a square can not be equal to a negative number) - if
 :
then
:
then  if and only if
if and only if  .
.
- if
 :
then
:
then  if and only if
if and only if

- if
-
Square root equations:

for which, depending on the sign of ,
,
- if
 :
then equation
:
then equation  has no solution
has no solution
(a square root can not be a negative number) - if
 :
then
:
then
 if and only if
if and only if
 and
and
 .
.
Note: Valeurs of for which
for which
 ,
quite appart from any equation,
are such that the quotient, are such that the square root
,
quite appart from any equation,
are such that the quotient, are such that the square root
 does not exist
(the square root of a negative number does not exist for real number !! ).
does not exist
(the square root of a negative number does not exist for real number !! ).
These values are prohibited values
for the expression
are prohibited values
for the expression
 and cannot, in any way, be solutions.
and cannot, in any way, be solutions.
- if
We now give an example for each type of equation.
Example 1:

 is a linear (or first degree) equation:
is a linear (or first degree) equation:
 .
.
Example 2:

 is a zero factor equation, thus
is a zero factor equation, thus

These two last equations are now simpler linear equations

Finally equation
 has two solutions:
has two solutions:
 and
and  .
.
Example 3:

 is a zero quotient equation, thus:
is a zero quotient equation, thus:

These two last equations can then simply be solved

 is the solution of the equation
is the solution of the equation
 ,
because we check that
,
because we check that
 (
(  is a prohibited value for the quotient).
is a prohibited value for the quotient).
Equation
 has thus a unique solution
has thus a unique solution  .
.
Example 4:

 is a (perfect) square equation
is a (perfect) square equation
 ,
with
,
with
 , thus :
, thus :

We can then solve these two last equations:
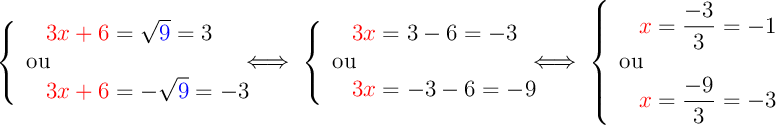
Thus, equation
 has two solutions
has two solutions  and
and  .
.
Example 5:

 is a square root equation:
is a square root equation:
 ,
with
,
with  :
:

First equation is a linear one and can simply be solved:

We moreover check that for
 ,
we have
,
we have
 .
.
Equation
 thus has a unique solution
thus has a unique solution  .
.
Exercices Solve the following equations:






















