Tous les devoirs de 2nde 
Tous les cours et exercices corrigés 
Télécharger le sujet du devoir 
Télécharger le corrigé du devoir 

Devoir de mathématiques

Y. Morel




Exercice 1. On considère les droites $\mathcal{D}$ et $\mathcal{D}'$ d'équations $\mathcal{D}: 2x+y=5$ et $\mathcal{D}': y=3x-1$.
  1. Déterminer les coordonnées du point $A$ d'intersection de $\mathcal{D}$ avec l'axe des ordonnées, et du point $B$ d'intersection de $\mathcal{D}$ avec l'axe des abscisses.
  2. Les droites $\mathcal{D}$ et $\mathcal{D}'$ sont-elles parallèles ?
  3. Tracer dans un repère les droites $\mathcal{D}$ et $\mathcal{D}'$.
  4. Calculer les coordonnées des éventuels points d'intersection de 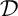$\mathcal{D}$ et $\mathcal{D}'$.




Exercice 2. Résoudre le système: $\la\bgar{ccr} 2x-y&=&7\\ -x+2y&=&-8 \enar\right.$

Exercice 3. J'ai dans ma poche deux pièces de monnaie, indiscernables au toucher. Une des deux pièces est bien équilibrée, l'autre est truquée: lorsqu'on la lance, on obtient "Pile" neuf fois sur dix.
Je prend une pièce au hasard dans ma poche et la lance. Quelle est la probabilité d'obtenir "Pile" ?

Exercice 4. On admet que, en France, dans la population d'enfants de 11 à 14 ans, le pourcentage d'enfants ayant déjà eu une crise d'asthme dans leur vie est de 13 %.
Un médecin d'une ville est surpris du nombre important d'enfants le consultant ayant des crises d'asthme et en informe les services sanitaires. Ceux-ci décident d'entreprendre une étude et d'évaluer la proportion d'enfants de 11 à 14 ans ayant déjà eu des crises d'asthme. Ils selectionnent de manière aléatoire 100 jeunes de 11 à 14 ans de la ville; sur ces 100 jeunes, 19 ont déjà eu des crises d'asthmes.
  1. Déterminer l'intervalle de fluctuation au seuil de 95 % de la proportion de jeunes de 11 à 14 ans ayant déjà eu une crise d'asthme dans un échantillon de 100 enfants.
  2. Que peut-on conclure de l'étude ?


Solution:


Corrigé du devoir de mathématiques

Y. Morel




Exercice 1. On considère les droites $\mathcal{D}$ et $\mathcal{D}'$ d'équations $\mathcal{D}: 2x+y=5$ et $\mathcal{D}': y=3x-1$.
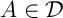  1. Soit $A(x;y)$ alors comme $A$ appartient à l'axe des ordonnées, on a $x=0$, et, comme $A\in\mathcal{D}$, $2x+y=5$ soit, avec $x=0$, $y=5$. Ainsi on trouve $A(0;5)$.
    Soit $B(x;y)$ alors comme $B$ appartient à l'axe des abscisses, on a $y=0$, puis comme $B\in\mathcal{D}$, $2x+y=5$ soit, avec $y=0$, $2x=5\iff x=\dfrac52$. Ainsi, on trouve $B\lp\dfrac52;0\rp$.
  2. $\mathcal{D}: 2x+y=5\iff y=-2x+5$ et $\mathcal{D}': y=3x-1$. $\mathcal{D}$ a pour coeeficient directeur $a=-2$ et $\mathcal{D}'$ a pour coefficient directeur $a'=3$. Ces coefficients directeurs sont différents, donc les droites sont sécantes.

  3. \[\psset{unit=.7cm,arrowsize=7pt} \begin{pspicture}(-1,-2)(4,5.5) \psline{->}(-1.2,0)(4,0) \psline{->}(0,-2)(0,6) \multido{\i=-1+1}{7}{\psline(.1,\i)(-.1,\i)\rput(-.2,\i){\i}} \multido{\i=-1+1}{5}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}} \psplot{-.5}{3}{-2 x mul 5 add}\rput(2.5,.8){$\mathcal{D}$} \psplot{-.3}{2}{3 x mul 1 sub}\rput(2.3,4.6){$\mathcal{D}'$} \end{pspicture}\]

  4. Soit $M(x;y)$ le point d'intersection de $\mathcal{D}$ et $\mathcal{D}'$, alors on a $\la\bgar{ccr} y&=&-2x+5\\ y&=&3x-1 \enar\right.$
    d'où $y=-2x+5=3x-1$ donc $5x=6\iff x=\dfrac65$, et alors $y=-2x+5=-2\tm\dfrac65+5=\dfrac{13}{5}$.
    Ainsi, le point d'intersection est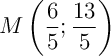 $M\lp\dfrac65;\dfrac{13}{5}\rp$.


Exercice 2. On a $ab'-a'b=2\tm2-(-1)\tm(-1)=3\not=0$ et donc ce système admet une unique solution.
$\la\bgar{ccr} 2x-y&=&7\\ -x+2y&=&-8 \enar\right. \iff \la\bgar{ccr} y&=&2x-7\\ y&=&\dfrac12x-4 \enar\right. $ On a ainsi $y=2x-7=\dfrac12x-4$, soit $\dfrac32x=3\iff x=2$, puis $y=2x-7=2\tm2-7=-3$. On trouve ainsi $x=2$ et $y=-3$.

Exercice 3.
\[\psset{xunit=1.5cm,yunit=1cm} \begin{pspicture}(-2,-3)(5,2.6) \psline(0,0)(1.5,1.5) \rput[l](1.8,1.5){Pièce truquée}\rput(0.7,1.2){$\dfrac12$} \psline(4,1.5)(5.5,2.25)\rput(5.75,2.25){$P$}\rput(4.7,2.2){$\dfrac{9}{10}$} \psline(4,1.5)(5.5,0.75)\rput(5.75,0.75){$F$}\rput(4.7,0.7){$\dfrac{1}{10}$} % \psline(0,0)(1.5,-1.5) \rput[l](1.6,-1.5){Pièce non truquée}\rput(0.7,-1.2){$\dfrac12$} \psline(4,-1.5)(5.5,-0.75)\rput(5.75,-0.75){$P$}\rput(4.7,-0.7){$\dfrac12$} \psline(4,-1.5)(5.5,-2.25)\rput(5.75,-2.25){$F$}\rput(4.7,-2.2){$\dfrac12$} \end{pspicture}\]

La probabilité d'obtenir "Pile" est alors $p=\dfrac12\tm\dfrac{9}{10}+\dfrac12\tm\dfrac12=\dfrac{14}{20} =\dfrac{7}{10}$

Exercice 4.
  1. L'intervalle de fluctation au seuil de 95 % d'une proportion $p=13\,\%$ sur un échantillon de $n=100$ jeunes est:
    \[I=\Bigl[ p - \dfrac{1}{\sqrt{n}} \ ;\ p + \dfrac{1}{\sqrt{n}} \Bigr] \simeq \Bigl[ 0,13-0,10\ ;\ 0,13 + 0,10\Bigr] \simeq \Bigl[ 0,03\ ;\ 0,23\Bigr]\]

  2. Lors de cette étude, $19\,\%=0,19$ de jeunes ont déjà eu une crise d'asthme. Comme $0,19\in I$, on ne peut pas conclure au fait que le nombre de jeunes ayant déjà eu une crise d'asthme dans cette ville soit particulièrement important; ce nombre qui paraît important pour le médecin peut s'expliquer par la fluctuation aléatoire d'un échantillon à l'autre de 100 jeunes.
    Le médecin n'a aucune raison d'être surpris.



Tous les devoirs de 2nde 
Tous les cours et exercices corrigés 
Télécharger le sujet du devoir 
Télécharger le corrigé du devoir