Etude de fonction
Etude à l'aide d'une fonction auxiliaire
Exercice corrigé - Etudes de fonctions, à l'aide d'une fonction auxiliaire et du théorème des valeurs intermédiaires
On considère la fonction
 .
.
On note
![]() sa courbe représentative dans un repère
sa courbe représentative dans un repère
![]() .
.
- A.
- Etude d'une fonction auxiliaire.
On pose
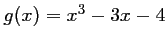 .
.
- Etudier le sens de variation de
 .
.
- Montrer que l'équation
 admet une unique solution,
que l'on notera
admet une unique solution,
que l'on notera  , dans l'intervalle
, dans l'intervalle ![$ [1;3]$](/Generateur-Devoirs/1S/Chap3/ex12_img10.png) .
.
- Donner un encadrement de
 à 0,1 près.
à 0,1 près.
- En déduire le signe de
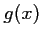 selon les valeurs de
selon les valeurs de 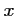 .
.
- Etudier le sens de variation de
- B.
- Etude des variations de
 .
.
Calculer
 , et montrer que
, et montrer que
 .
En déduire le tableau de variation de
.
En déduire le tableau de variation de  .
.
- C.
- Tangente.
Déterminer l'équation de la tangente
 à
à
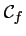 au point
d'abscisse 2.
au point
d'abscisse 2.
Autres ressources, exercices, cours, …