Fonction avec deux paramètres

Ajustement à l'aide d'une tangente

Exercice corrigé - Dérivée d'une fonction avec deux paramètres à déterminer ensuite grâce à la connaissance d'une tangente


Soit $ \mathcal{C}$ la représentation graphique de la fonction $ f$ définie sur $ {\rm I\kern-.1567em R}\setminus\left\{2\right\}$ par:

$\displaystyle f(x)=\dfrac{x^2+ax+b}{x-2} \qquad a,b\ \in{\rm I\kern-.1567em R}\ . $

  1. Calculer $ f'(x)$ .
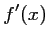  2. Déterminer $ a$ et $ b$ tels que la droite d'équation $ y=8$ soit tangente à $ \mathcal{C}$ au point d'abscisse 3.

Autres ressources, exercices, cours, …