Produit scalaire
Détermination de la mesure d'un angle à l'aide du produit scalaire
Exercice corrigé - Produit scalaire - Calcul de la mesure d'un angle entre deux vecteurs dans un repère à l'aide du produit scalaire
Dans un repère orthonormé
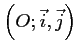 ,
on considère le vecteur
,
on considère le vecteur
Déterminer une mesure de l'angle
![]() à un
degré près.
à un
degré près.
Autres ressources, exercices, cours, …