Deux suites récurrentes imbriquées

Exercice corrigé sur les suites

Exercice corrigé sur les suites: deux suites imbriquées définies par récurrence. Utilisation de suites intermédiaires, géométrique et constante, et détermination des expressions explicites, en fonction de n


On considère les suites $\left( u_n\rp$ et $\left( v_n\rp$ définies par leur premier terme $u_0=1$ et $v_0=2$ et, pour tout entier $n$,

\[\la\begin{array}{ll} u_{n+1}=\dfrac13u_n+\dfrac23v_n\\[.8em] v_{n+1}=\dfrac15u_n+\dfrac45v_n\enar\right.\]
  1. Calculer $u_1$ et $v_1$.
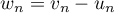  2. On pose, pout tout entier $n$, $w_n=v_n-u_n$.
    1. Calculer $w_0$ et $w_1$.
    2. Montrer que la suite $\left( w_n\rp$ est géométrique. Préciser sa raison et son premier terme.
      Donner alors l'expression explicite de $w_n$ en fonction de $n$.
  3. On pose, pour tout entier $n$, $t_n=3u_n+10v_n$.
    1. Calculer $t_0$ et $t_1$.
    2. Montrer que la suite $\left( t_n\rp$ est constante.
  4. Exprimer alors, explicitement en fonction de $n$, les termes $u_n$ et $v_n$.
  5. Quelles sont les limites de ces deux suites ?

Autres ressources, exercices, cours, …