Exercice Bac STI2D & STL - juin 2016

Suite géométrique et algorithme

Exercice corrigé du bac STI2D / STL - Métropole juin 2016 - suite, algorithmique et suite géométrique


Un centre de vacances possède une piscine de $600\,\text{m}^3$ soit 600 000 litres. L'eau du bassin contient du chlore qui joue le rôle de désinfectant. Toutefois le chlore se dégrade et 25 % de celui-ci disparaît chaque jour, en particulier sous l'effet des ultra-violets et de l'évaporation. Le 31 mai à 9 h, le responsable analyse l'eau du bassin à l'aide d'un kit distribué par un magasin spécialisé.
Le taux de chlore disponible dans l'eau est alors de 1,25 mg/L (milligrammes par litre).
Document
$${|*{3}{c|}} \multicolumn{3}{c}{\textbf{R\'eglementation des piscines publiques}} \\\hline Param\`etres contr\^ol\'es & Seuils de qualit\'e r\'eglementaire &Incidences sur la qualit\'e de l'eau \\ \hline & Au minimum 2 mg/L & $< 2$ mg/L : sous-chloration\\ &&Risque de prolif\'eration\\ &&bact\'erienne dans l'eau \\ \hline Pr\'esence de Chlore &Au maximum 4 mg/L& $> 4$ mg/L: surchloration \\ &&Irritation de la peau\\ \hline \multicolumn{3}{r}{\textbf{Source : Agence R\'egionale de Sant\'e}} $$

À partir du $1^\text{er}$ juin pour compenser la perte en chlore, la personne responsable de l'entretien ajoute, chaque matin à 9h, 570g de chlore dans la piscine.
Pour le bien-être et la sécurité des usagers, le responsable souhaite savoir si cet apport journalier en chlore permettra de maintenir une eau qui respecte la réglementation donnée par l' Agence Régionale de Santé pour les piscines publiques.


Partie A


  1. Pour tout entier naturel $n$ on note $u_n$ la quantité de chlore disponible, exprimée en grammes, présente dans l'eau du bassin le $n$-ième jour suivant le jour de l'analyse, immédiatement après l'ajout de chlore. Ainsi $u_0$ est la quantité de chlore le 31 mai à 9 h et $u_1$ est la quantité de chlore le 1$^\text{er}$ juin à 9h après l'ajout de chlore.
    1. Montrer que la quantité de chlore, en grammes, présente dans l'eau du bassin le 31 mai à 9h est $u_0 = 750$.
      Au regard des recommandations de l'agence régionale de santé, le responsable pouvait-il donner l'accès à la piscine le 31 mai ?
    2. Montrer que $u_1 = 1132,5$.
    3. Justifier que pour tout entier naturel $n$, $u_{n+1} = 0, 75u_n + 570$.
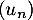    4. La suite $\left(u_n\right)$ est-elle géométrique ?

  2. Soit l'algorithme ci-dessous :

    \[\begin{array}{|l |l |}\hline \text{Variables } &u : \text{un nombre r\'eel }\\ &N : \text{un nombre entier naturel }\\ &k : \text{un nombre entier naturel }\\ \text{ Initialisation :} &\text{Saisir la valeur de } N \\ & u \text{ prend la valeur } 750 \\ \text{ Traitement :} &\text{ Pour } k \text{ allant de } 1 \text{ \`a } N\\ &\hspace{0,5cm} u\text{ prend la valeur } 0,75 u +570\\ &\text{ Fin du Pour }\\ \text{ Sortie : }& \text{ Afficher } u \\\hline \end{array}\]

    1. Quel est le rôle de cet algorithme ?
    2. Recopier et compléter le tableau suivant, par des valeurs exactes, en exécutant cet algorithme « pas à pas » pour $N = 3$.
      \[\begin{array}{|c|c|c|c|c|}\hline \text{Variables } & \text{ Initialisation } & \text{ Étape 1 } & \text{ Étape 2 } & \text{ Étape 3 } \\ \hline u & 750 &1132,5& & \\ \hline \end{array}\]

      Au regard des recommandations de l'agence régionale de santé, au bout de combien de jours la piscine peut-elle être ouverte ?
    3. Calculer une valeur approchée à $10^{-3}$ près de la quantité de chlore le 15$^\text{\`eme}$ jour juste après l'ajout de chlore.




Partie B


Au fil du temps, la quantité de chlore évolue. On note $d_n$ l'écart de quantité de chlore d'un jour à l'autre en grammes. Pour tout entier naturel $n$, on a $d_n = u_{n+1}- u_n$.
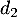    1. Calculer $d_0, d_1$ et $ d_2$. On donnera une valeur exacte.
    2. Justifier que 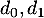$d_0, d_1$ et $ d_2$ semblent être les termes d'une suite géométrique.
  2. Vérifier que $u_{n+1}- u_n = -0,25u_n + 570$.
  3. On admet que pour tout entier naturel $n$, on a $d_{n+1}= 0, 75d_n$.
    1. Justifier que $d_n = 382,5 \times 0, 75^n$.
    2. En déduire que pour tout entier naturel 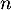$n$, on a $u_n = 2280 - 1530\times 0,75^n$.
    3. Déterminer la limite de la suite $\left( u_n\rp$. Interpréter le résultat trouvé.

Autres ressources, exercices, cours, …