Exercice type Bac - Nombres complexes
Polynôme complexe et géométrie dans le plan complexe
Exercice corrigé type Bac: Nombres complexes, polynôme et géométrie dans le plan complexe
On considère le polynôme
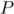défini par:
;
.
- Calculer
et 
,
puis trouver un polynôme 
du second degré à coefficients réels
tel que, pour tout 
,
on ait 
.
- Résoudre dans
l'équation 
.
- Placer dans le plan complexe rapporté au repère orthonormal
les points 
, 
, 
et 
d'affixes
respectives
, 
,
et 
,
puis montrer que ces quatre points appartiennent à un même cercle.
- On note
le symétrique de 
par rapport à 
.
Conjecturer la nature du triangle
,
puis démontrer votre conjecture.
Autres ressources, exercices, cours, …