Bac S 2014 - Géométrie dans l'espace

Géométrie dans un tétraèdre

Exercice corrigé Bac S, métropole juin 2014: géométrie dans l'espace, dans un tétraèdre


Dans l'espace, on considère un tétraèdre $ABCD dont les faces $ABC, $ACD et $ABD sont des triangles rectangles et isocèles en A. On désigne par $E, $F et $G les milieux respectifs des côtés $[AB], $[BC] et $[CA].


On choisit $AB pour unité de longueur et on se place dans le repère orthonormé $\left( A;\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\rp de l'espace.


  1. On désigne par $\mathcal{P} le plan qui passe par A et qui est orthogonal à la droite (DF).
    On note H le point d'intersection du plan $\mathcal{P} et de la droite (DF).
    1. Donner les coordonnées des points D et F.
    2. Donner une représentation paramétrique de la droite (DF).
    3. Déterminer une équation cartésienne du plan $\mathcal{P}.
    4. Calculer les coordonnées du point H.
    5. Démontrer que l'angle $\widehat{\text{EHG}} est un angle droit.
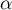  2. On désigne par $M un point de la droite $(DF) et par $t le réel tel que $\overrightarrow{DM} = t\overrightarrow{DF}. On note $\alpha la mesure en radians de l'angle géométrique $\widehat{EMG}.
    Le but de cette question est de déterminer la position du point $M pour que $\alpha soit maximale.
    1. Démontrer que $ME^2 = \dfrac{3}{2}t^2-\dfrac{5}{2}t+\dfrac{5}{4}.
    2. Démontrer que le triangle $MEG est isocèle en $M. En déduire que $ME\sin \lp\dfrac{\alpha}{2}\rp=\dfrac{1}{2\sqrt{2}}.
    3. Justifier que $\alpha est maximale si et seulement si $\sin \lp\dfrac{\alpha}{2} \rp est maximal.
      En déduire que $\alpha est maximale si et seulement si $ME^2 est minimal.
    4. Conclure.

Autres ressources, exercices, cours, …