Bac S 2010 - Géométrie dans l'espace

Représentation paramétrique d'une droite

Exercice corrigé Bac S, 2010: Représentation paramétrique d'une droite, distance minimale


Bac S, septembre 2010 4 points
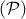L'espace est rapporté à un repère orthonormal . Soit le plan d'équation : 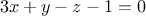et 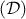la droite dont une représentation paramétrique est


    1. Le point C(1 ; 3 ; 2) appartient-il au plan ? Justifier.
    2. Démontrer que la droite est incluse dans le plan .
  2. Soit le plan passant par le point C et orthogonal à la droite .
    1. Déterminer une équation cartésienne du plan .
    2. Calculer les coordonnées du point I, point d'intersection du plan et de la droite .
    3. Montrer que CI .
  3. Soit un nombre réel et le point de la droite de coordonnées .
    1. Vérifier que pour tout nombre réel .
    2. Montrer que CI est la valeur minimale de C lorsque décrit l'ensemble des nombres réels.

Autres ressources, exercices, cours, …