Exercice Bac S septembre 2019 - Intégration

Intégrale gaussienne - Encadrements et algorithme de Monté Carlo

Exercice corrigé Bac S juin 2019, septembre - Intégrale gaussienne, expontielle, encadrements, et algorithme de Monté Carlo


On donne ci-dessous la représentation graphique $\mathcal{C}_g$ dans un repère orthogonal d'une fonction $g$ définie et continue sur $\R$. La courbe $\mathcal{C}_g$ est symétrique par rapport à l'axe des ordonnées et se situe dans le demi-plan $y>0$.

\[\psset{xunit=3cm,yunit=6cm,comma=true} \begin{pspicture}(-2,-0.25)(2,1.2) \multido{\n=-2.0+0.5}{9}{\psline[linewidth=0.2pt](\n,-0.2)(\n,1.2)} \multido{\n=-0.2+0.2}{8}{\psline[linewidth=0.2pt](-2,\n)(2,\n)} \psaxes[linewidth=1.25pt,Dx=0.5,Dy=0.2](0,0)(-2,-0.19)(2,1.2) \uput[d](-0.08,-0.02){$0$} \psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-2}{2}{1 2.71828 x dup mul exp div} %\psGauss[mue=0,sigma=0.75,linewidth=1.25pt,linecolor=blue]{-2}{2} \end{pspicture}\]

Pour tout $t\in\R$ on pose:
\[G(t)=\int_0^t g(u) du\]


Partie A

Les justifications des réponses aux questions suivantes pourront s'appuyer sur des considérations graphiques.
  1. La fonction $G$ est-elle croissante sur $[0~;~ +\infty[$ ? Justifier.
  2. Justifier graphiquement l'inégalité $G(1) \leqslant 0,9$.
  3. La fonction $G$ est-elle positive sur $\R$ ? Justifier.

Dans la suite du problème, la fonction $g$ est définie sur $\R$ par $g(u) = e^{-u^2}$.

Partie B
  1. Étude de $g$
    1. Déterminer les limites de la fonction $g$ aux bornes de son ensemble de définition.
    2. Calculer la fonction dérivée de $g$ et en déduire le tableau de variations de $g$ sur $\R$.
    3. Préciser le maximum de $g$ sur $\R$. En déduire que $g(1)\leqslant1$.
  2. On note $E$ l'ensemble des points $M$ situés entre la courbe $\mathcal{C}_g$, l'axe des abscisses et les droites d'équation $x=0$ et $x=1$. On appelle $I$ l'aire de cet ensemble.
    On rappelle que:
    \[I=G(1)=\int_0^1 g(u) du\]

    On souhaite estimer l'aire $I$ par la méthode dite "de Monte-Carlo" décrite ci-dessous.
    • On choisit un point $M(x~;~y)$ en tirant au hasard de façon indépendante ses coordonnées $x$ et $y$ selon la loi uniforme sur l'intervalle $[0~;~ 1]$. On admet que la probabilité que le point $M$ appartienne à l'ensemble $E$ est égale à $I$.
    • On répète $n$ fois l'expérience du choix d'un point $M$ au hasard. On compte le nombre $c$ de points appartenant à l'ensemble $E$ parmi les $n$ points obtenus.
    • La fréquence $f = \dfrac{c}{n}$ est une estimation de la valeur de $I$.

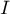    1. La figure ci-dessous illustre la méthode présentée pour $n = 100$. Déterminer la valeur de $f$ correspondant à ce graphique.

      \[\psset{xunit=11.5cm,yunit=9cm,comma=true} \begin{pspicture}(-0.05,-0.05)(1.05,1.05) \psframe(1,1) \psaxes[Dx=0.2,Dy=0.2](0,0)(0,0)(1,1) \psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1}{1 2.71828 x dup mul exp div} \psdots(0.1,0.98)(0.05,0.02)(0.12,0.9)(0.22,0.83)(0.32,0.82)(0.37,0.815)(0.09,0.76)(0.22,0.69)(0.35,0.67)(0.11,0.7)(0.18,0.53)(0.24,0.63)(0.57,0.61)(0.64,0.61)(0.65,0.6)(0.21,0.58) (0.48,0.55)(0.64,0.55)(0.66,0.53)(0.7,0.5)(0.57,0.44)(0.72,0.44)(0.77,0.44)(0.85,0.47) (0.13,0.46)(0.75,0.39)(0.54,0.41)(0.09,0.28)(0.27,0.29)(0.69,0.36)(0.7,0.37)(0.08,0.35) (0.28,0.28)(0.46,0.25)(0.47,0.23)(0.57,0.28)(0.7,0.28)(0.96,0.25)(0.3,0.23)(0.46,0.23) (0.54,0.21)(0.93,0.2)(0.96,0.23)(0.025,0.16)(0.035,0.16)(0.18,0.18)(0.28,0.16)(0.41,0.12) (0.63,0.16)(0.95,0.1)(0.45,0.13)(0.74,0.17)(0.94,0.12)(0.96,0.15)(0.08,0.04)(0.29,0.04) (0.01,0.02)(0.12,0.02)(0.51,0.01)(0.58,0)(0.92,0)(0.28,0.4)(0.3,0.42)(0.32,0.45) (0.35,0.5)(0.37,0.55)(0.39,0.57)(0.41,0.5)(0.48,0.41)(0.79,0.2)(0.76,0.15)(0.8,0.1) (0.85,0.26)(0.9,0.4)(0.44,0.65)(0.44,0.48)(0.57,0.63) \psdots[dotstyle=o](0.29,0.95)(0.57,0.98)(0.59,0.95)(0.79,0.92)(0.9,0.99)(0.49,0.8)(0.68,0.9)(0.79,0.91)(0.81,0.92)(0.43,0.85)(0.77,0.79)(0.94,0.77)(0.84,0.68)(0.87,0.64)(0.85,0.61)(0.83,0.59) (0.74,0.77)(0.97,0.69)(0.975,0.495)(0.92,0.47)(0.93,0.44)(0.6,0.8)(0.68,0.78) \end{pspicture}\]


    2. L'exécution de l'algorithme ci-dessous utilise la méthode de Monte-Carlo décrite précédemment pour déterminer une valeur du nombre $f$. Recopier et compléter cet algorithme.


      $f$, $x$ et $y$ sont des nombres réels, $n$, $c$ et $i$ sont des entiers naturels.
      ALEA est une fonction qui génère aléatoirement un nombre compris entre $0$ et $1$.

      \[\fbox{\begin{minipage}{8cm} $c \gets 0$\\ Pour $i$ variant de $1$ \`a $n$ faire :\\ \hspace*{2.cm}$x \gets$ ALEA\\ \hspace*{2.cm}$y \gets$ ALEA\\ \hspace*{1cm}Si $y \leqslant \ldots$ alors\\ \hspace*{2.cm}$c \gets \ldots$\\ \hspace*{1cm}fin Si\\ fin Pour\\ \hspace{2.5cm}$f \gets \ldots$\\ \end{minipage}}\]


    3. Une exécution de l'algorithme pour $n=1000$ donne $f = 0,757$. En déduire un intervalle de confiance, au niveau de confiance de 95 %, de la valeur exacte de $I$.


Partie C
On rappelle que la fonction $g$ est définie sur $\R$ par $g(u) = \text{e}^{-u^2}$ et que la fonction $G$ est définie sur $\R$ par :
\[G(t) =\int_0^t g(u) du\]

On se propose de déterminer une majoration de $G(t)$ pour $t \geqslant 1$.


  1. Un résultat préliminaire.
    On admet que, pour tout réel $u \geqslant 1$, on a $g(u) \leqslant \dfrac1{u^2}$.
    En déduire que, pour tout réel $t \geqslant 1$, on a :
    \[\int_1^t g(u) du \leqslant 1 - \dfrac1t\]

  2. Montrer que, pour tout réel $t \geqslant 1$,
    \[G(t) \leqslant 2 - \dfrac1t\]

    Que peut-on dire de la limite éventuelle de $G(t)$ lorsque $t$ tend vers $+\infty$ ?

Autres ressources, exercices, cours, …