Exercice type Bac
Suite de probabilités - Loi binomiale
Exercice corrigé type Bac: suite de probabilités - Loi binomiale
Dans une foire, une publicité annonce: « Un billet sur deux est gagnant, achetez deux billets !».
Dans cet exercice, on suppose qu'effectivement, sur le nombre de billets en vente, exactement un billet sur deux est gagnant. Xavier est toujours le premier acheteur de la journée.
Calculer la probabilité qu'il ait au moins un billet gagnant (donner le résultat sous forme de fraction).
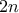billets sont mis en vente
(
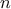est un entier naturel).
Xavier achète deux billets.
- Démontrer que la probabilité
qu'il achète au moins un
billet gagnant est:
.
- Calculer
et expliquer ce résultat.
- Démontrer que, pour tout entier naturel
non nul,
.
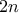billets sont mis en vente
(
est un entier naturel non nul).
Xavier revient chaque jour, pendant 3 jours, acheter deux billets.
- Quelle est la probabilité
qu'il obtienne, au cours de ces
3 jours, au moins un billet gagnant ?
- Etudier la limite de la suite
.
Autres ressources, exercices, cours, …