Exercice Bac S Amérique du nord, juin 2016
Volume d'un récupérateur d'eau
Exercice corrigé Bac S Amérique du nord, juin 2016: Etudes de fonctions avec un logarithme, calculs de pentes, tangentes, primitive, et intégrales
Un particulier veut faire fabriquer un récupérateur d'eau. Ce récupérateur d'eau est une cuve qui doit respecter le cahier des charges suivant:
- elle doit être située à deux mètres de sa maison;
- la profondeur maximale doit être de deux mètres;
- elle doit mesurer cinq mètres de long;
- elle doit épouser la pente naturelle du terrain.
Cette cuve est schématisée ci-contre.
![$$(-1.8,-0.5)(7,5)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\pspolygon(2,0)(2,1.8)(-1.3,2.5)(-1.3,0.7)
\rput(-3.3,0.7){\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}}
\psline(2.1,2.7)(5.4,2)
\psline(-1.3,2.5)(2.1,2.7)
\psline(2,1.8)(5.4,2)
\psline[linewidth=0.5pt](2,1.8)(2,3)\psline[linewidth=0.5pt](-1.3,2.5)(-1.3,3.7)
\psset{arrowsize=2pt 3}
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(2,3)(-1.3,3.7)
\psline[linewidth=0.5pt](2,1.8)(1.2,1.75)\psline[linewidth=0.5pt](2,0)(1.2,-0.05)
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(1.2,1.75)(1.2,-0.05)
\uput[l](1.2,0.85){2 m}\uput[u](1.35,3.35){5 m}
$$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/1.png)
La partie incurvée est modélisée par la courbe
La courbe
On considère les points
(-0.2,-0.25)(6,2.5)
\psaxes[linewidth=1.25pt](0,0)(0,0)(6,2.5)
\uput[u](2.8,0.2){$\mathcal{C}_f$}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\psframe[fillstyle=solid,fillcolor=lightgray](2,2)
\psdots(2,2)(5.437,2)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psplot[plotpoints=4000]{3}{5.8}{x 2 add 5.437 sub}
\uput[u](2,2){$A$}
\uput[u](5.437,2){$B$}
\uput[ul](5.75,2.2){$\mathcal{T}$}
\uput[dl](2,0){$I$}
\uput[dr](3.437,0){$D$}
\rput(1,1){Terrain}
\rput(3.2,1.2){Cuve}
\rput(4.7,0.5){Terrain}
\psline[linestyle=dotted,linewidth=1.5pt](2,2)(5.437,2)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/10.png)
Partie A L'objectif de cette partie est d'évaluer le volume de la cuve.
- Justifier que les points
 et
et 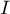 appartiennent à la courbe
appartiennent à la courbe
 et que l'axe des abscisses est tangent à la courbe
et que l'axe des abscisses est tangent à la courbe
 au point
au point  .
.
- On note
 la tangente à la courbe
la tangente à la courbe  au
point
au
point  , et
, et  le point d'intersection de la droite
le point d'intersection de la droite  avec l'axe des abscisses.
avec l'axe des abscisses.
- Déterminer une équation de la droite
 et en
déduire les coordonnées de
et en
déduire les coordonnées de  .
.
- On appelle
 l'aire du domaine délimité par la courbe
l'aire du domaine délimité par la courbe
 , les droites d'équations
, les droites d'équations  ,
,  et
et  .
.
 peut être encadrée par l'aire du triangle
peut être encadrée par l'aire du triangle  et celle du
trapèze
et celle du
trapèze  .
.
Quel encadrement du volume de la cuve peut-on en déduire ?
- Déterminer une équation de la droite
-
- Montrer que, sur l'intervalle
![$[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/31.png) ,
la fonction
,
la fonction  définie par
définie par
![\[G(x)=\dfrac{x^2}{2}\ln \lp\dfrac{x}{2}\rp-\dfrac{x^2}{4}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/33.png)
est une primitive de la fonction définie par
définie par
 .
.
- En déduire une primitive
 de la fonction
de la fonction  sur
l'intervalle
sur
l'intervalle ![$[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/38.png) .
.
- Déterminer la valeur exacte de l'aire
 et en déduire une
valeur approchée du volume
et en déduire une
valeur approchée du volume  de la cuve au
de la cuve au  près.
près.
- Montrer que, sur l'intervalle
Partie B Pour tout réel
On admet que, pour tout réel
{\n}}
}
\pspolygon[fillstyle=solid,fillcolor=gray](2,0.1)(2,1.5)(0.35,2.3)(0.35,0.9)
\pspolygon[fillstyle=solid,fillcolor=gray](2,1.5)(0.35,2.3)(3.37,2.47)(5.08,1.7)
\pscustom[fillstyle=solid,fillcolor=gray]{
\pscurve(2,0.1)(3,0.316)(4,0.87)(5.08,1.75)
\psline(5.08,1.75)(2,1.5)
}
\pspolygon(5.437,2.1)(2,1.85)(0.35,2.7)(3.787,2.95)
\psline(2,1.85)(2,1.5)
\psline(0.35,2.7)(0.35,2.3)
\pscurve(0.35,0.9)(1.35,1.16)(2.35,1.72)(3.35,2.5)(3.787,2.95)
\psline[linestyle=dotted,linewidth=1.5pt](5.08,0.2)(5.08,1.75)(0,1.37)
\uput[d](5.2,0.3){$x$}
\uput[l](0,1.37){$f(x)$}
\multido{\n=0+1}{4}{\uput[l](0,\n){\n}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/50.png)
- Quel volume d'eau, au m
 près, y a-t-il dans la cuve lorsque
la hauteur d'eau dans la cuve est de un mètre ?
près, y a-t-il dans la cuve lorsque
la hauteur d'eau dans la cuve est de un mètre ?
- On rappelle que
 est le volume total de la cuve,
est le volume total de la cuve, 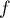 est la
fonction définie en début d'exercice et
est la
fonction définie en début d'exercice et  la fonction définie dans
la partie B.
la fonction définie dans
la partie B.
On considère l'algorithme ci-dessous.
Interpréter le résultat que cet algorithme permet d'afficher.
Variables: a est un réel
b est un réelTraitement: a prend la valeur 2
b prend la valeur 2e
Tant que v(b)-v(a)>10-3 faire:
c prend la valeur (a+b)/2Fin Tant que
Si v(c)<V/2, alors:
a prend la valeur cSinonb prend la valeur cFin SiSortie: Afficher f(c)
Autres ressources, exercices, cours, …