Oral du Bac - Probabilité continues

Loi normale - Détermination de l'écart type

Oral du Bac: Probabilités continues, loi normale d'écart-type à déterminer

Soit

une variable aléatoire qui suit la loi normale d'espérance $$\mu=6$ et d'écart-type $$\sigma=0,3$ .

Calculer la probabilité $$P\left( X\in\bigl[5,\!7\,;\,6,\!3\bigr]\rp$
On souhaite modifier l'écart-type de la variable aléatoire 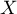de telle sorte que

$P\left( X\in\bigl[5,\!7\,;\,6,\!3\bigr]\rp=0,95$

La variable aléatoire suit donc désormais la loi normale d'espérance et d'écart-type inconnu.
1. Quelle est la loi suivie par la variable aléatoire $$Z=\dfrac{X-6}{\sigma}$ ?
2. Exprimer la probabilité $$P\left( X\in\bigl[5,\!7\,;\,6,\!3\bigr]\rp$ à l'aide de la variable aléatoire .
3. Déterminer l'écart-type $$\sigma$ .

Autres ressources, exercices, cours, …