Restitutions Organisées des connaissances (ROC)

Les incontournables à connaître

Y. Morel




Introduction - Que faire avec ces ROC - Pourquoi apprendre ça ?


Dans cette page sont contenues toutes les ROC (Restitution organisée des Connaissances) indiquées explicitement dans le nouveau programme de terminale S entré en vigueur à la rentrée 2012.
Toutes ces ROC sont à connaître impérativement. Elles sont exigibles le jour du bac (et éventuellement lors d'un oral de rattrapage). Cela ne signifie pas que la connaissance de ces quelques démonstrations soit suffisante pour appréhender correctement le programme de terminale S.

Pourquoi apprendre ces démonstrations ?

Pour plusieurs raisons:
  • La réponse la plus "simpliste et dénuée de sens" (mathématique mais pas que) est qu'elles sont exigibles au bac, que chaque année, sur chaque sujet, un exercice (ou partie) porte dessus.
    Il faut donc les connaître...
  • Ces démonstrations sont à travailler et à être connues car elles contiennent des éléments clés sur le programme de terminale.
    C'est en se frottant à celles-ci que l'on peut savoir si on maîtrise effectivement les connaissances mathématiques requises, pour la démonstration en question certes, mais aussi pour aborder d'autres types d'exercices, de problèmes, ...
  • Utiliser et appliquer une propriété ou un théorème demande de connaître un ensemble d'hypothèses à vérifier (qui consituent d'une certaine façon son domaine d'application ou de validité).
    C'est en travaillant et comprenant sa démonstration que l'on peut comprendre clairement l'utilité de chacune de ses hypothèses, pourquoi elles sont nécessaires, pourquoi la propriété devient fausse si on en oublie une, ...
  • Souvent, quand on ne sait pas résoudre un problème, répondre à une question, c'est parce que "on ne sait pas comment commencer", "on n'a pas d'idée"...
    Les démonstrations contiennent justement ces idées. Cette question me fait penser à tel théorème ou telle propriété ? Alors j'ai une idée pour l'attaquer: celle contenue dans sa démonstration.
    Pour cette raison, entre autre, il est donc conseillé d'apprendre non pas chaque démonstration par coeur, mais d'essayer de prendre du recul, et de retenir surtout l'idée principale (de la même façon qu'on n'apprend pas par cœur une œuvre complète d'un écrivain ou d'un philosophe, mot à mot, mais qu'on se concentre plus sur la synthèse de son, ou ses, idées directrices).

    En générale, au niveau terminale S, une démonstration = une idée, le reste de la démonstration étant constitué de calculs ou d'application d'autres résultats connus.
  • Enfin, sans sa démonstration, une propriété se réduit à une simple recette de cuisine. On peut encore l'utiliser, l'appliquer, mais au prix fort: il faut être exactement dans le cadre imposé par la recette, une hypothèse non satisfaite, un élément manquant et celle-ci doit-être purement et simplement abondonnée.
    En connaissant la démonstration, son mécanisme, même si la propriété n'est pas directement utilisable, on a une chance de pouvoir néanmoins l'adapter au cas précis que l'on a sous les yeux. Les conclusions ne seront certainement pas les mêmes, mais peut-être peuvent-elles alors suffire pour résoudre le problème.
Pour toutes ces raisons, il est donc largement conseillé de bien travailler et connaître ces démonstrations, qui valent donc largement autant que de faire et refaire des exercices plus ou moins "types", et du coup, est largement aussi conseillé de ne pas s'arrêter uniquement à ces quelques maigres démonstrations pointées du doigt par le programme, et donc de revenir sur ses cours, et de s'attabler sérieusement devant toutes les démonstrations.

Suites

Propriété

Si $(u_n)$ et $(v_n)$ sont deux suites telles que
  • à partir d'un certain rang, $u_n\geqslant v_n$,
  • $\dsp\lim_{n\to+\infty} v_n=+\infty$

alors, $\dsp\lim_{n\to+\infty} u_n=+\infty$.


Démonstration: Comme $\dsp\lim_{n\to+\infty} v_n=+\infty$, tout intervalle $]A;+\infty[$, $A\in{\rm I\kern-.1567em R}$, contient tous les $v_n$ à partir d'un rang $n_0$.

C'est-à-dire que, dès que $n\geqslant n_0$, on a $v_n>A$.

Or, à partir d'un certain rang, que l'on peut noter $n_1$, $_n\geqslant v_n$.

Ainsi, si on note $N$ le plus grand des rangs $n_0$ et $n_1$, on a, pour tout rang $ n\geqslant N$, $u_n\geqslant v_n>A$.

En d'autres termes, tout intervalle $]A;+\infty[$ contient tous les $ u_n$ à partir du rang $N$, ce qui est la définition de $\dsp\lim_{n\to+\infty} u_n=+\infty$. $\square$

Propriété

Si une suite est croissante et converge vers un réel $ l$ , alors tous les termes de la suite sont inférieurs ou égaux à $ l$.


Démonstration: Raisonnement par l'absurde:

Supposons qu'il existe un rang $ p$ pour lequel $ u_p>l$ . Alors, il existe un réel $ \alpha>0$ tel que $ u_p=l+\alpha$ .


Comme $ u_n$ est croissante, pour tout $ n\geqslant p$ , on a alors $ u_n\geqslant u_p=l+\alpha$ .


D'autre part, comme $ (u_n)$ converge vers $ l$ , tout intervalle ouvert du type $ ]l-\varepsilon ;l+\varepsilon [$ , $ \varepsilon >0$ , contient tous les termes $ u_n$ à partir d'un certain rang.

Comme cela est vrai pour tout réel $ \varepsilon >0$ , on peut choisir par exemple $ \varepsilon =\alpha$ , et il existe donc un rang $ n_0$ à partir duquel tous les termes $ u_n$ sont dans l'intervalle $ ]l-\alpha;l+\alpha[$ . En particulier, dès que $ n\geqslant n_0$ , on a $ u_n<l+\alpha$ .


Si maintenant $ N$ désigne le plus grand des rangs $ n_0$ et $ p$ , on doit avoir, dès que $ n\geqslant N$ (c'est-à-dire, dès que $ n\geqslant n_0$ et $ n\geqslant p$ ), $ u_n<l+\alpha$ et $ u_n>u_p=l+\alpha$ , ce qui est impossible.


Ainsi, l'hypothèse de départ: «il existe un rang $ p$ pour lequel $ u_p>l$ »est fausse, et donc pour tout rang $ n$ , $ u_n\leqslant l$ . $ \square$

Propriété

Si $ q>1$ , alors $ \displaystyle \lim_{n\to+\infty} q^n=+\infty$ .


Démonstration: $ q>1$ , alors il existe un réel $ \alpha>0$ tel que $ q=1+\alpha$ .

Alors $ q^n=(1+\alpha)^n$ .


Démontrons par récurrence que, pour tout entier naturel $ n$ , $ (1+\alpha)^n\geqslant 1+n\alpha$ .


Initialisation: Pour $ n=0$ , $ (1+\alpha)^0=1$ et d'autre part $ 1+n\alpha=1$ , et on a donc bien ainsi $ (1+\alpha)^n\geqslant 1+n\alpha$ .


Hérédité: Supoposons que pour un certain entier $ n$ , on ait $ (1+\alpha)^n\geqslant 1+n\alpha$ .

Alors, au rang $ n+1$ ,

$ (1+\alpha)^{n+1}=(1+\alpha)^n(1+\alpha)$ , or, d'après l'hypothèse de récurrence, $ (1+\alpha)^n\geqslant 1+n\alpha$ , et ainsi,

$ (1+\alpha)^{n+1}=(1+\alpha)^n(1+\alpha) \geqslant (1+n\alpha)(1+\alpha) =1+(n+1)\alpha+n\alpha^2 $ .

De plus, pour tout entier $ n$ , $ n\alpha^2\geqslant 0$ , et donc, $ 1+(n+1)\alpha+n\alpha^2\geqslant 1+(n+1)\alpha$ .

Ainsi, $ (1+\alpha)^{n+1}\geqslant 1+(n+1)\alpha$ , ce qui montre que la propriété est encore vraie au rang $ n+1$ .


Conclusion: D'après le principe de récurrence, on a donc démontré que, pour tout entier $ n$ , $ (1+\alpha)^n\geqslant 1+n\alpha$ .



On a donc, pour tout entier $ n$ , $ q^n=(1+\alpha)^n\geqslant 1+n\alpha$ .

Or, comme $ \alpha>0$ , on a $ \displaystyle \lim_{n\to+\infty} 1+n\alpha=+\infty$ , et alors, d'après le théorème de comparaison (corollaire du théorème des gendarmes), $ \displaystyle \lim_{n\to+\infty} q^n=\lim_{n\to+\infty} (1+\alpha)^n=+\infty$ . $ \square$

Propriété

Toute suite croissante non majorée tend vers $ +\infty$.


Démonstration: Soit $ (u_n)$ une suite croissante et non majorée.

Alors, comme $ (u_n)$ n'est pas majorée, pour tout réel $ A$ , il existe un rang $ N$ tel que $ u_N>A$ .


De plus, $ (u_n)$ est croissante, et donc, pour tout rang $ n\geqslant N$ , on a $ u_n\geqslant u_N>A$ .


Ceci étant vrai pour tout réel $ A$ , cela signifie exactement que tout intervalle ouvert $ ]A;+\infty[$ contient tous les termes $ u_n$ à partir d'un certain rang $ N$ , et donc que $ \displaystyle \lim_{n\to+\infty} u_n=+\infty$ . $ \square$



Fonction exponentielle

Propriété

Il existe une unique fonction $ f$ dérivable sur $ {\rm I\kern-.1567em R}$ telle que $ f'=f$ et $ f(0)=1$.


Démonstration: $ \bullet$ L'existence d'une telle fonction est admise, conformément au programme.


$ \bullet$ Unicité:

Soit $ f$ et $ g$ deux fonctions telles que $ f'=f$ et $ f(0)=1$ , $ g'=g$ et $ g(0)=1$ .


La fonction $ g$ ne s'annule pas sur $ {\rm I\kern-.1567em R}$ . En effet, si on définit la fonction $ \varphi $ par $ \varphi (x)=g(x)\times g(-x)$ , alors $ \varphi $ est dérivable sur $ {\rm I\kern-.1567em R}$ avec $ \varphi '(x)=g'(x)\times g(-x)+ g(x)\times \left[-g'(x)\right]$ , or $ g'=g$ , et donc, $ \varphi '(x)=g(x)\times g(-x)-g(x)\times g(-x)=0$ .

Ainsi, $ \varphi $ est constante, or $ \varphi (0)=g(0)\times g(-0)=\left[g(0)\right]^2=1$ , et donc, pour tout réel $ x$ , $ \varphi (x)=g(x)\times g(-x)=1$ .

En particulier, il ne peut exister de réel $ x$ tel que $ g(x)=0$ (car on aurait alors $ \varphi (x)=g(x)\times g(-x)=0\not=1$ ).



On peut alors définir la fonction $ h=\dfrac{f}{g}$ , qui est bien définie et dérivable sur $ {\rm I\kern-.1567em R}$ car $ g$ ne s'annule pas.

De plus,

$\displaystyle h'=\dfrac{f'g-fg'}{g^2}=\dfrac{fg-fg}{g^2}=0\ ,\ $    car $\displaystyle f'=f$    et $\displaystyle g'=g\ . $

Ainsi, $ h$ est constante sur $ {\rm I\kern-.1567em R}$ , avec $ h(0)=\dfrac{f(0)}{g(0)}=\dfrac{1}{1}=1$ , d'où, pour tout réel $ x$ , $ h(x)=\dfrac{f(x)}{g(x)}=1 \iff f(x)=g(x)$ .

On a donc $ f=g$ : il n'exsite qu'une unique fonction $ f$ vérifiant $ f'=f$ et $ f(0)=1$ . $ \square$

Propriété

$ \displaystyle \lim_{n\to+\infty} e^x=+\infty$ et $ \displaystyle \lim_{n\to-\infty} e^x=0$.


Démonstration: On démontre pour cela que, pour tout réel $ x$ , $ e^x>x$ .


Soit la fonction $ f$ définie sur $ {\rm I\kern-.1567em R}$ par $ f(x)=e^x-x$ .

Alors, $ f$ est dérivable sur $ {\rm I\kern-.1567em R}$ avec $ f'(x)=e^x-1$ , et

  • $ f'(x)>0\iff e^x-1>0\iff e^x>1=e^0\iff x>0$ , car la fonction exponentielle est strictement croissantee sur $ {\rm I\kern-.1567em R}$.
  • De même, $f'(x)<0\iff e^x-1<0\iff e^x<1=e^0\iff x<0$ , car la fonction exponentielle est strictement croissantee sur ${\rm I\kern-.1567em R}$.

On peut ainsi dresser le tableau de variation de $ f$ :

$\displaystyle \begin{tabular}{\vert c\vert ccccc\vert}\hline $x$\ & $-\infty$\... ...-0.4)&& \psline{->}(-0.6,-0.4)(0.5,0.5)& \\ &&&1&& \\ \hline \end{tabular} $

On en déduit que $ 1$ est le minimum global de $ f$ sur $ {\rm I\kern-.1567em R}$ , et donc que, pour tout réel $ x$ , $ f(x)=e^x-x\geqslant 1$ .

En particulier, pour tout réel $ x$ , $ f(x)e^x-x>0 \iff e^x>x$ .


Comme $ \displaystyle \lim_{x\to+\infty} x=+\infty$ , on a donc, d'après le théorème de comparaison (corollaire du théorème des gendarmes), $ \displaystyle \lim_{x\to+\infty} e^x=+\infty$ .



Pour la limite de la fonction exponentielle en $ -\infty$ , on utilise alors le fait que, pour tout réel $ x$ , $ e^{-x}=\dfrac{1}{e^x}$ .

Ainsi, si on pose $ X=-x$ , on a: $ \displaystyle \lim_{x\to-\infty} e^x =\lim_{X\to+\infty} e^{-X} =\lim_{X\to+\infty} \dfrac{1}{e^X} =0 $ . $ \square$



Intégration

Propriété

Soit $f$ une fonction continue et positive sur $[a;b]$.


La fonction $ F$ définie sur $ [a;b]$ par $\displaystyle F(x)=\int_a^x f(t)\,dt$ est dérivable sur $[a;b]$ et a pour dérivée $ f$.


Démonstration: On démontre cette propriété dans le cas où $ f$ est une fonction continue, positive et croissante sur $ [a;b]$ (conformément au programme, le cas général étant admis).


Soit $ x_0$ un réel de $ [a;b]$ et $ h>0$ tel que $ x_0+h\in[a;b]$ .

On a, d'après la relation de Chasles pour les intégrales:

$\displaystyle F(x_0+h)-F(x_0) =\int_a^{x_0+h} f(t)\,dt - \int_a^{x_0} f(t)\,dt =\int_a^{x_0+h} f(t)\,dt + \int_{x_0}^a f(t)\,dt =\int_{x_0}^{x_0+h} f(t)\,dt $

$ f$ étant croissante sur $ [a;b]$ , on a l'encadrement:

$\displaystyle \left(x_0+h-x_0\right)f(x_0) \leqslant \int_{x_0}^{x_0+h} f(t)\,dt \leqslant \left(x_0+h-x_0\right)f(x_0+h) $

soit,

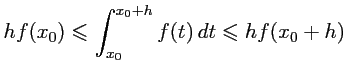
$\displaystyle h f(x_0)\leqslant \int_{x_0}^{x_0+h} f(t)\,dt \leqslant hf(x_0+h) $

ou encore, en divisant par $ h>0$ ,

$\displaystyle f(x_0)\leqslant \dfrac{\displaystyle \int_{x_0}^{x_0+h} f(t)\,dt}{h} \leqslant f(x_0+h) $

soit encore, puisque $ \displaystyle F(x_0+h)-F(x_0) =\int_{x_0}^{x_0+h} f(t)\,dt $ ,

$\displaystyle f(x_0)\leqslant \dfrac{F(x_0+h)-F(x_0)}{h}\leqslant f(x_0+h) $

En procédant de même pour $ h<0$ , on obtient que $ \displaystyle f(x_0+h)\leqslant \dfrac{F(x_0+h)-F(x_0)}{h}\leqslant f(x_0) $ .



Comme $ f$ est continue sur $ [a;b]$ , donc en particulier en $ x_0$ , on a $ \displaystyle \lim_{h\to0} f(x_0+h)=f(x_0)$ , et donc, d'après le théorème des gendarmes, $ \displaystyle \lim_{h\to0} \dfrac{F(x_0+h)-F(x_0)}{h}=f(x_0)$ .

$ F$ est donc dérivable en $ x_0$ , avec $ F'(x_0)=f(x_0)$ .

Ceci étant vrai pour tout $ x_0\in[a;b]$ , on en déduit que $ F$ est dérivable sur $ [a;b]$ et que $ F'=f$ . $ \square$

Propriété

Toute fonction continue sur un intervalle $ I$ admet des primitives sur $ I$.


Démonstration: On se place dans le cas où $ I=[a;b]$ et $ f$ admet un minimum $ m$ sur $ I$ .


La fonction $ g$ définie sur $ I$ par $ g(x)=f(x)-m$ est donc continue et positive sur $ I$ .

Elle admet donc une primitive $ G$ sur $ I$ (donnée par $ \displaystyle G(x)=\int_a^x g(t)\,dt$ .)


La fonction $ F$ définie par $ F(x)=G(x)-mx$ et alors une primitive de $ f$ car,

$\displaystyle F'(x)=G'(x)-m=g(x)-m=f(x)\ ,$

ce qui montre que $ f$ admet bien des primitives sur $ I$ . $ \square$



Géométrie vectorielle dans l'espace

Le théorème dit du "toit" permet de démontrer que des droites dans l'espace sont parallèles ou concourantes en un point.

Propriété

Théorème «du toit») Si trois plans $ P$, $ Q$ et $ R$ de l'espace sont sécants deux à deux, alors les trois droites d'intersection sont concourantes ou parallèles.


Démonstration: On note $d_1=P\cap Q$ la droite intersection des plans $P$ et $ Q$ , $ d_2=Q\cap R$ la droite intersection des plans $ Q$ et $ R$ , et $d_3=P\cap R$ la droite intersection des plans $P$ et $R$.

Considérons, par exemple, dans un premier temps, les droites $d_1$ et $ d_2$. Comme ces deux droites sont coplanaires (elles appartiennent au même plan $Q$), seulement deux cas sont possibles: les droites $ d_1$ et $ d_2$ sont sécantes ou bien elles sont parallèles (si ces deux droites n'étaient pas coplanaires, elles pourraient aussi n'être ni sécantes, ni parallèles).

1 $ ^{\text{er}}$ Cas:
Supposons $ d_1$ et $ d_2$ sécantes.
\begin{pspicture}(-3,-1.5)(7,4.5) \psplot{-3}{7}{0.25 x mul -0.5 add}\rput(-3,-... ... (0,-0.5)(-0.66,3.22)(4.2,1.6)(4.5,0.625) % \rput(6,1.2){$I$} \end{pspicture}

Soit $ I=d_1\cap d_2$ le point d'intersection des deux droites $ d_1$ et $ d_2$ .

On a alors, $ I\in d_1$ , donc $ I\in P$ , car $ d_1\subset P$ , et de même, $ I\in d_2$ , donc $ I\in R$ , car $ d_2\subset R$ .

Ainsi, $ I$ est un point commun aux plans $ P$ et $ R$ , soit $ I\in P\cap R$ .

Par conséquent, $ I$ appartient aussi à la droite $ d_3$ qui est l'intersection des plans $ P$ et $ R$ .

On en conclut donc que le point $ I$ appartient à la fois aux trois droites $ d_1$ , $ d_2$ et $ d_3$ , et donc que ces trois droites sont bien concourantes en $ I$ .



2 $ ^{\text{e}}$ Cas:
Supposons $ d_1$ et $ d_2$ parallèles.
\begin{pspicture}(-4,-0.5)(7,4) \psline(-4,1)(7,1)\rput(-3.5,1.2){$d_1$} \psli... ...=red](0,0)(-1,3)(5,3)(6,0) \rput(0.2,0.2){\textcolor{red}{$R$}} \end{pspicture}

Raisonnons par l'absurde et supposons que les droites $ d_1$ et $ d_3$ sont sécantes en un point $ J$ .

On aurait alors, $ J\in d_1$ , donc $ J\in Q$ , et de même, $ J\in d_3$ , donc $ J\in R$ .

Ainsi, $ J$ appartiendrait à la fois aux plans $ Q$ et $ R$ , et donc à la droite $ d_2$ , intersections de $ Q$ et $ R$ .

Le point appartiendrait alors aux droites $ d_1$ et $ d_2$ , ce qui contredit notre hypothèse: $ d_1$ et $ d_2$ sont parallèles.

Les droites $ d_1$ et $ d_3$ ne peuvent donc pas être sécantes et, comme elles appartiennent au même plan $ P$ , elles sont donc parallèles.


Par conséquent, on en conclut que les trois droites $ d_1$ , $ d_2$ et $ d_3$ sont parallèles.

$ \square$



Produit scalaire dans l'espace

L'espace est muni d'un repère orthonormé.

Propriété

(1)
Un plan de l'espace de vecteur normal $ \vec{n}\left(a;b;c\right)$ a une équation cartésienne de la forme $ ax+by+cz+d=0$.
(2)
Réciproquement, $ a$ , $ b$ , $ c$ et $ d$ étant quatre nombres, $ a$ , $ b$ et $ c$ étant non tous nuls, l'ensemble des points $ M(x;y;z)$ tels que $ ax+by+cz+d=0$ est un plan de vecteur normal $ \vec{n}\left(a;b;c\right)$.


Démonstration: (1) Un point $ M(x;y;z)$ appartient au plan $ \mathcal{P}$ passant par $ A(x_A;y_A;z_A)$ si, et seulement, $ \overrightarrow{AM}\cdot\vec{n}=0 \iff a(x-x_A)+b(x-x_B)+c(x-x_D)=0 \iff ax+by+c+d=0 $ , où on a posé $ d=-ax_A-by_A-cz_A$ .



(2) Soit $ \mathcal{P}$ l'ensemble des points $ M(x;y;z)$ tels que $ ax+by+cz+d=0$ .

Les réels $ a$ , $ b$ et $ c$ étant non tous nuls, on peut supposer que, par exemple, $ a\not=0$ .

Alors, le point $ A\left(-\dfrac{d}{a};0;0\right)$ est un point de l'ensemble $ \mathcal{P}$ , car $ a\left(-\dfrac{d}{a}\right)+b\times 0+c\times 0+d=0$ .

On a de plus alors,

$\displaystyle ax+by+cz+d=0 \iff a\left(x+\dfrac{d}{a}\right)+by+cz=0 \iff \overrightarrow{AM}\cdot\vec{n}=0 $

avec le vecteur $ \vec{n}(a;b;c)$ .

Ainsi, $ \mathcal{P}$ est le plan passant par $ A$ et de vecteur normal $ \vec{n}$ . $ \square$

Propriété

Une droite $ \mathcal{D}$ est orthogonale à toute droite d'un plan $ \mathcal{P}$ si et seulement si elle est orthogonale à deux droites sécantes de ce plan.


Démonstration: Condition nécessaire. Si la droite $ \mathcal{D}$ est orthogonale à toute droite du plan $ \mathcal{P}$ alors elle l'est en particulier à deux droites quelconques du plan $ \mathcal{P}$ (sécantes ou non d'ailleurs).



Condition suffisante. Supposons, réciproquement, que la droite $\mathcal{D}$ soit orthogonale à deux droites sécantes $ \mathcal{D}_1$ et $ \mathcal{D}_2$ du plan $ \mathcal{P}$ .

On considère alors une droite $ \Delta$ quelconque du plan $ \mathcal{P}$ .


Soit $ \vec{u}$ , $ \vec{u}_1$ , $ \vec{u}_2$ et $ \vec{v}$ des vecteurs directeurs respectifs des droites $ \Delta$ , $ \mathcal{D}_1$ , $ \mathcal{D}_2$ et $ \mathcal{D}$ .

Le couple $ \left(\vec{u}_1;\vec{u}_2\right)$ dirige le plan $ \mathcal{P}$ , et donc, il existe deux réels $ \alpha$ et $ \beta$ tels que $ \vec{u}=\alpha\vec{u}_1+\beta\vec{u}_2$ .

De plus, comme $ \mathcal{D}$ est orthogonale à $ \mathcal{D}_1$ et $ \mathcal{D}_2$ , on a $ \vec{v}\cdot\vec{u}_1=\vec{v}\cdot\vec{u}_2=0$ , et alors

$\displaystyle \vec{v}\cdot\vec{u} =\vec{v}\cdot\left(\alpha\vec{u}_1+\beta\vec{u}_2\right) =\alpha\vec{v}\cdot\vec{u}_1+\beta\vec{v}\cdot\vec{u}_2 =0 $

ce qui montre la droite $ \mathcal{D}$ est orthogonale à la droite $ \Delta$ . $ \square$



Probabilités


Conditionnement, indépendance

Propriété

Si deux événements $A$ et $B$ sont indépendants, alors il en est de même pour les événements $ \overline{A}$ et B$.


Démonstration: Soit $ A$ et $ B$ deux événements indépendants.


$ A\cap B$ et $ \overline{A}\cap B$ forment une partition de $ B$ , et donc, $ P(B)=P(A\cap B)+P(\overline{A}\cap B)$ , soit $ P(\overline{A}\cap B)=P(B)-P(A\cap B)$ .

Or, $ A$ et $ B$ étant indépendants, on a $ P(A\cap B)=P(A)\times P(B)$ , et donc,

$\displaystyle P(\overline{A}\cap B) =P(B)-P(A\cap B) =P(B)-P(A)\times P(B) =P(B)\Bigl( 1-P(A)\Bigr) =P(B)\times P(\overline{A}) $

ce qui montre que les événements $ \overline{A}$ et $ B$ sont indépendants. $ \square$


Probabilités continues

Propriété

L'espérance d'une variable aléatoire $X$ suivant la loi exponentielle de paramètre $ \lambda $ est $ E(X)=\dfrac{1}{\lambda }$.


Démonstration: Soit $ X$ une variable aléatoire suivant la loi exponentielle de paramètre $ \lambda $ , alors la densité de probabilité de $ X$ est la fonction définie sur $ [0;+\infty[$ par $ f(x)=\lambda e^{-\lambda x}$ .


L'espérance de $ X$ est alors

$\displaystyle E(x) =\lim_{x\to+\infty}\int_0^{x} t\,f(t)\,dt =\lim_{x\to+\infty}\int_0^{x} t\,\lambda e^{-\lambda t}\,dt $

Pour calculer cette intégrale, on peut chercher une primitive de $ g(t)=\lambda te^{-\lambda t}$ sous la forme $ G(t)=(at+b)e^{-\lambda t}$ , où $ a$ et $ b$ sont des nombres réels à déterminer.


On a alors, $ G'(t)=ae^{-\lambda t}+(at+b)\left(-\lambda e^{-\lambda t}\right) =\Bigl( -\lambda at +\left(a-\lambda b\right)\Bigr) e^{-\lambda t} $ .

Ainsi, $ G$ est une primitive de $ g$ si, et seulement si, $ \left\{\begin{array}{ll} -\lambda a=\lambda \\ a-\lambda b=0 \end{array}\r... ...left\{\begin{array}{ll} a=-1 \\ b=-\dfrac{1}{\lambda } \end{array}\right. $ .

Donc, pour tout $ t\geqslant 0$ , $ G(t)=\left(-t-\dfrac{1}{\lambda }\right)e^{-\lambda t}$ est une primitive de $ f(t)=\lambda t e^{-\lambda t}$ , et alors

$\displaystyle E(X) =\lim_{x\to+\infty}\int_0^{x} t\,\lambda e^{-\lambda t}\,dt... ...to+\infty} \Bigl( G(x)-G(0)\Bigr) =\lim_{x\to+\infty} \Bigl( G(x)-G(0)\Bigr) $

or, $ G(0)=-\dfrac{1}{\lambda }$ , et $ \displaystyle \lim_{x\to+\infty} e^{-\lambda x}=0$ et $ \displaystyle \lim_{x\to+\infty} xe^{-\lambda x}=0$ , d'où $ \displaystyle \lim_{x\to+\infty} G(x)=0$ .

Ainsi, au final, $ E(X)=\dfrac{1}{\lambda }$ . $ \square$

Propriété

Soit $ X$ une variable aléatoire suivant la loi normale centrée réduite $ \mathcal{N}(0;1)$, alors pour tout réel $\alpha\in]0;1[$, il existe un unique réel $u_\alpha>0$ tel que $ P\left(-u_\alpha\leqslant X\leqslant u_\alpha\right)=1-\alpha$.


Démonstration: Par symétrie de la densité de probabilité $ f$ de la loi normale centrée réduite, on a

$\displaystyle P\left(-u\leqslant X\leqslant u\right)=2\,P\left(0\leqslant X\leqslant u\right) =2\int_0^u f(x)\,dx=2F(u)\ , $

où $ F$ est la primitive de $ f$ sur $ {\rm I\kern-.1567em R}$ qui s'annule en 0 .


$ F$ est continue (et même dérivable) et croissante sur $ [0;+\infty[$ car $ F'=f$ et $ f>0$ .

De plus, $ \displaystyle \lim_{u\to+\infty} G(u)=\dfrac12$ : il s'agit de l'aire sous la courbe de $ f$ qui est symétrique par rapport à l'axe des ordonnées et dont l'aire totale (de $ -\infty$ à $ +\infty$ ) vaut $ 1$ .

On a donc le tableau de variation de la fonction $ 2F$ :

$\displaystyle \begin{tabular}{\vert c\vert ccc\vert}\hline $x$\ & $0$\ &\hspac... ...\\ $2F$\ && \psline{->}(-0.8,-0.3)(1,0.5)&\\ &0&& \\ \hline \end{tabular} $

Comme pour tout nombre $ \alpha\in]0;1[$ , le nombre $ 1-\alpha\in]0;1[$ , d'après le théorème des valeurs intermédiaires, il existe un unique $ u_\alpha\in]0;+\infty[$ tel que $ 2F\left(u_\alpha\right)=1-\alpha$ , c'est-à-dire tel que
$ P\left(-u_\alpha\leqslant X\leqslant u_\alpha\right)=1-\alpha$ . $ \square$



Intervalle de fluctuation

Propriété

Soit $X_n$ une variable aléatoire suivant la loi binomiale $ \mathcal{B}(n;p)$, alors pour tout $ \alpha\in]0;1[$, on a

$\displaystyle \lim_{n\to+\infty} P\left(\frac{X_n}{n}\in I_n\right)=1-\alpha$

où $ I_n$ désigne l'intervalle

$\displaystyle \left[ p-u_\alpha\frac{\sqrt{p(1-p)}}{\sqrt{n}}\,;\, p+u_\alpha\frac{\sqrt{p(1-p)}}{\sqrt{n}} \right]$

avec $ u_\alpha$ le nombre tel que, si $ X$ suit la loi normale $ \mathcal{N}(0;1)$,

$\displaystyle P(-u_\alpha\leqslant X\leqslant u_\alpha)=1-\alpha$

L'intervalle $I_n$ s'appelle l'intervalle de fluctuation au seuil $ 1-\alpha$.



Démonstration: Si $ X_n$ suit la loi binomiale $ \mathcal{B}(n;p)$ , alors d'après le théorème de Moivre-Laplace, pour $ n$ assez grand, $ X_n$ suit approximativement la loi normale $ \mathcal{N}(np;\sqrt{np(1-p)})$ , et donc, la variable aléatoire $ \dfrac{X_n}{n}$ suit approximativement la loi normale $ \mathcal{N}\left(\dfrac{np}{n};\dfrac{\sqrt{np(1-p)}}{n}\right)$ , soit la loi normale $ \mathcal{N}\left(p;\sigma\right)$ , avec $ \sigma=\sqrt{\dfrac{p(1-p)}{n}}$ .


On cherche alors $ \delta$ tel que

$\displaystyle P\left(p-\delta\leqslant \dfrac{X_n}{n}\leqslant p+\delta\right) =1-\alpha $

En ramenant la variable $ \dfrac{X_n}{n}$ à une variable suivant la loi normale réduite $ \mathcal{N}(0;1)$ :

$\displaystyle P\left(-\frac{\delta}{\sigma}\leqslant \dfrac{\dfrac{X_n}{n}-p}{\sigma}\leqslant \frac{\delta}{\sigma}\right) =1-\alpha $

La variable aléatoire $ \displaystyle X=\dfrac{\dfrac{X_n}{n}-p}{\sigma}$ suit une loi normale centrée réduite $ \mathcal{N}(0;1)$ , et on sait donc qu'il existe un unique nombre $ u_\alpha$ tel que

$\displaystyle P(-u_\alpha\leqslant X\leqslant u_\alpha)=1-\alpha\,. $


Le théorème est donc vérifié pour $ \dfrac{\delta}{\sigma}=u_\alpha$ , soit $ \delta=u_\alpha\sigma=u_\alpha\sqrt{\dfrac{p(1-p)}{n}}$ , et on a donc, pour $ n$ assez grand,

$\displaystyle P\left(\frac{X_n}{n}\in I_n\right)=1-\alpha $

$ \square$



Estimation

Propriété

On considère la variable aléatoire $X$ qui à tout échantillon de taille  $ n$ associe le nombre d'individus possédant le caractère étudié. On suppose que $X$ suit une loi binomiale $ \mathcal{B}(n,f)$, et on note $ f'=\dfrac{X}{n}$ la fréquence du caractère dans l'échantillon.

Alors, pour $n$ assez grand, l'intervalle

$\displaystyle I_n=\left[f'-\dfrac{1}{\sqrt{n}}\,;\,f'+\dfrac{1}{\sqrt{n}}\right]\,.$

contient la fréquence $f$ du caractère dans la population avec une probabilité supérieure ou égale à 0,95.

L'intervalle $I_n$ s'appelle l'intervalle au niveau de confiance de 95%.


Démonstration: La fréquence $ f'$ du caractère dans l'échantillon est une valeur prise par la variable aléatoire $ \dfrac{X}{n}$ . Elle est ou n'est pas dans l'intervalle $ \left[f-\dfrac{1}{\sqrt{n}}\,;\,f+\dfrac{1}{\sqrt{n}}\right]$ , mais on sait que 95% des fréquences des échantillons sont dans cet intervalle.


De plus,

\begin{displaymath}\begin{array}{ll} f\in \left[f'-\dfrac{1}{\sqrt{n}}\,;\,f'+\... ...\sqrt{n}}\leqslant f \end{array}\right.\\ [0.3cm] \end{array}\end{displaymath}

Et on a donc,

$\displaystyle f'\in \left[f-\dfrac{1}{\sqrt{n}}\,;\,f+\dfrac{1}{\sqrt{n}}\right] \iff f\in \left[f'-\dfrac{1}{\sqrt{n}}\,;\,f'+\dfrac{1}{\sqrt{n}}\right] $

Ainsi, $ f$ sera dans 95% des intervalles du type $ I_n=\left[f'-\dfrac{1}{\sqrt{n}}\,;\, f'+\dfrac{1}{\sqrt{n}}\right]$ . $\square$



Haut de la page Top link / Haut de la page


LongPage: h2: 1 - h3: 1