Calcul du barême de points de handicap suivant l'écart de classement
Y. Morel
Aller directement à la l'outil de calculs en ligne
Position du problème
Dans tous les sports existe un système de classement officiel. Le classement d'une personne donne une évaluation de son niveau dans la pratique de ce sport, niveau en particulier comparativement à celui des autres.
Ainsi, si deux adversaires s'affrontent, on s'attend "normalement" à ce que celui de plus haut classement l'emporte.
Ce "normalement" exprime, les joueurs le savent bien, un critère statistique et probabiliste.
Plus le classement de mon adversaire est fort par rapport au mien, mois j'ai de chances de gagner. Une telle rencontre sportive est donc dès le départ déséquilibrée.
Les règles du jeu sont très généralement symétriques afin d'assurer un minimum d'équité (les mêmes pièces aux échecs, l'alternance des services et des changements de côtés au tennis, le changement de côté à la mi-temps au foot, la mesure de la vitesse du vent lors des championnats d'athlétisme, … ).
On peut donc aussi se poser la question de cette équité face aux classements, ou plutôt de: comment rétablir cette équité face aux éventuels déséquilibres de classement ?
Dans les sports ou jeux ou il a un décompte de points, mettons que le premier à 10 l'emporte, quel handicap doit-on attribuer au joeur de meilleur classement afin que la probabilité que chacun l'emporte soit égale ?
Modèle et paramètres - Partie classique, sans handicap
La question portant sur un nombre de points de handicap, il est naturel d'utiliser comme paramètre de base non pas la probabilité de victoire d'une partie complète, mais la probabilité de victoire d'un seul point.
On note dans toute la suite
On notera de plus
Exemple simple d'une partie en  points
points
Pour une partie en deux points, le premier arrivant à 2 ayant gagné, la situation se représente à l'aide d'un arbre. Le joueur A affronte le joeur B, chaque branche représente l'issue d'un point disputé. Le vainqueur du point est indiqué à l'extrémité. En indice, le score est indiqué, score de A en premier. À chaque point, indépendamment les uns des autres, le joueur
{$A_{1/0}$}\rput(.4,.65){$p$}
\rput[l](1.1,-1){$B_{0/1}$}\rput(.4,-.7){$q$}
\psline(3,1.5)(2,1)(3,.5)
\rput[l](3.1,1.5){\blue$A_{2/0}$}\rput(2.5,1.4){$p$}
\rput[l](3.1,.5){$B_{1/1}$}\rput(2.5,.5){$q$}
\psline(3,-1.5)(2,-1)(3,-.5)
\rput[l](3.1,-.5){$A_{1/1}$}\rput(2.5,-.6){$p$}
\rput[l](3.1,-1.5){\red$B_{0/2}$}\rput(2.5,-1.5){$q$}
\psline(5,1)(4,.5)(5,.5)
\rput[l](5.1,1){\blue$A_{2/1}$}\rput(4.5,.9){$p$}
\rput[l](5.1,.5){\red$B_{1/2}$}\rput(4.5,.25){$q$}
\psline(5,-1)(4,-.5)(5,-.5)
\rput[l](5.1,-.5){\blue$A_{2/1}$}\rput(4.5,-.3){$p$}
\rput[l](5.1,-1){\red$B_{1/2}$}\rput(4.5,-1.){$q$}
\end{pspicture}\]](fich-IMG/7.png)
Sa probabilité de victoire de la rencontre est, somme des probabilités des événements en bleu (formule des probabilités totales, pour être savant),
![\[\bgar{ll}P_2&=p\tm p+p\tm q\tm p+q\tm p\tm p\\[.6em]
&=p^2+2p^2q\enar\]](fich-IMG/8.png)
Deuxième exemple avec  points
points
On peut traîter de même ce cas suivant, du premier qui arrive à 3 points afin d'essayer d'en déduire une formule générale pour le cas
{$A_{1/0}$}
\rput[l](1.1,-2){$B_{0/1}$}
%
\psline(3,2.5)(2,2)(3,1.5)
\rput[l](3.2,2.5){$A_{2/0}$}
\rput[l](3.2,1.5){$B_{1/1}$}
%
\psline(3,-2.5)(2,-2)(3,-1.5)
\rput[l](3.2,-1.5){$A_{1/1}$}
\rput[l](3.2,-2.5){$B_{0/2}$}
%
\psline(5,3)(4,2.5)(5,2.5)
\rput[l](5.2,3){\blue$A_{3/0}$}
\rput[l](5.2,2.5){$B_{2/1}$}
\psline(7,3)(6,2.5)(7,2.5)
\rput[l](7.2,3){\blue$A_{3/1}$}
\rput[l](7.2,2.5){$B_{2/2}$}
\psline(9,3)(8,2.5)(9,2.5)
\rput[l](9.2,3){\blue$A_{3/2}$}
\rput[l](9.2,2.5){\red$B_{2/3}$}
%
\psline(5,2)(4,1.5)(5,1)
\rput[l](5.2,2){$A_{2/1}$}
\rput[l](5.2,1){$B_{1/2}$}
\psline(7,2)(6,2)(7,1.5)
\rput[l](7.2,2){\blue$A_{3/1}$}
\rput[l](7.2,1.5){$B_{2/2}$}
\psline(9,2)(8,1.5)(9,1.5)
\rput[l](9.2,2){\blue$A_{3/2}$}
\rput[l](9.2,1.5){\red$B_{2/3}$}
%
\psline(7,1)(6,1)(7,.5)
\rput[l](7.2,1){$A_{2/2}$}
\rput[l](7.2,.5){\red$B_{1/3}$}
\psline(9,1)(8,1)(9,.5)
\rput[l](9.2,1){\blue$A_{3/2}$}
\rput[l](9.2,.5){\red$B_{2/3}$}
%%
\psline(5,-3)(4,-2.5)(5,-2.5)
\rput[l](5.2,-3){\red$B_{0/3}$}
\rput[l](5.2,-2.5){$A_{1/2}$}
\psline(7,-3)(6,-2.5)(7,-2.5)
\rput[l](7.2,-2.5){$A_{2/2}$}
\rput[l](7.2,-3){\red$B_{1/3}$}
\psline(9,-3)(8,-2.5)(9,-2.5)
\rput[l](9.2,-2.5){\blue$A_{3/2}$}
\rput[l](9.2,-3){\red$B_{2/3}$}
%
\psline(5,-2)(4,-1.5)(5,-1)
\rput[l](5.2,-1){$A_{2/1}$}
\rput[l](5.2,-2){$B_{1/2}$}
\psline(7,-2)(6,-2)(7,-1.5)
\rput[l](7.2,-2){\red$B_{1/3}$}
\rput[l](7.2,-1.5){$A_{2/2}$}
\psline(9,-2)(8,-1.5)(9,-1.5)
\rput[l](9.2,-2){\red$B_{2/3}$}
\rput[l](9.2,-1.5){\blue$A_{3/2}$}
%
\psline(7,-1)(6,-1)(7,-.5)
\rput[l](7.2,-1){$B_{2/2}$}
\rput[l](7.2,-.5){\blue$A_{3/1}$}
\psline(9,-1)(8,-1)(9,-.5)
\rput[l](9.2,-.5){\blue$A_{3/2}$}
\rput[l](9.2,-1){\red$B_{2/3}$}
\end{pspicture}\]](fich-IMG/11.png)
Pour gagner,
- soit gagner 3 points successivement sans jamais perdre de point;
il y a une seule telle façon, de probabilité
 ;
;
- gagner 3 points et en perdre 1 (score 3/1);
il y a 3 telles façons: perdre le 1er point, le 2ème ou le 3ème.
Chaque tel chemin a une probabilité

- gagner 3 points et en perdre 2 (score 3/2):
il y a
 telles façons: le nombre de façons de
positionner les 2 points perdus sur 5 points joués.
Chaque tel chemin a une probabilité
telles façons: le nombre de façons de
positionner les 2 points perdus sur 5 points joués.
Chaque tel chemin a une probabilité 
On note le coefficient binomial égal au nombre de façons de choisir
le coefficient binomial égal au nombre de façons de choisir  éléments parmi
éléments parmi  .
.
Généralisation: partie en  points
points
Le raisonnement précédent se généralise. Pour gagner une partie en
- gagner
 points et n'en perdre aucun. Il y a une seule telle façon, de probabilité
points et n'en perdre aucun. Il y a une seule telle façon, de probabilité 
- gagner
 points et en perdre un seul. Il y a
points et en perdre un seul. Il y a
 façons: les façons de choisir où le point est perdu parmi les
façons: les façons de choisir où le point est perdu parmi les  points joués, sauf le dernier que
points joués, sauf le dernier que  doit forcément gagner pour remporter la partie.
doit forcément gagner pour remporter la partie.
Chaque chemin a une probabilité .
.
- gagner
 points et en perdre 2. Il y a
points et en perdre 2. Il y a
 façons: les façons de choisir où les 2 points perdus se sitent parmi les
façons: les façons de choisir où les 2 points perdus se sitent parmi les  points joués (
points joués ( moins le dernier)
moins le dernier)
Chaque chemin a une probabilité .
.
- …
- gagner
 points et en perdre
points et en perdre  . Il y a
. Il y a
 façons: les façons de choisir où les
façons: les façons de choisir où les 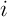 points perdus se sitent parmi les
points perdus se sitent parmi les  points joués (
points joués ( moins le dernier)
Chaque chemin a une probabilité
moins le dernier)
Chaque chemin a une probabilité  .
.
En ajoutant toutes ces probabilités, on trouve que
![\[\bgar{ll}P_N&=p^N+
\lp\bgar{c}N\\1\enar\rp p^Nq^1+
\lp\bgar{c}N+1\\2\enar\rp p^Nq^2+\dots\\[1.2em]
&=\dsp\sum_{i=0}^{N-1}\lp\bgar{c}N+i-1\\i\enar\rp p^Nq^i\enar\]](fich-IMG/45.png)
Partie avec points de handicap
On garde les mêmes notations que précédemment, et on considère que
Par exemple, pour la partie en
{\small$0/1$}
\psline(1,1)(0,0)(1,-1)
\rput[l](1.1,1){$A_{1/1}$}
\rput[l](1.1,-1){\red$B_{0/2}$}
\psline(3,1.5)(2,1)(3,.5)
\rput[l](3.1,1.5){\blue$A_{2/1}$}
\rput[l](3.1,.5){\red$B_{1/2}$}
\end{pspicture}\]](fich-IMG/51.png)
et la probabilité de victoire pour
On généralise ce résultat, en notant
![\[P(N,H)=\dsp\sum_{i=0}^{N-1-H}\lp\bgar{c}N+i-1\\i\enar\rp p^Nq^i\]](fich-IMG/59.png)
Partie équitable
La question se pose maintenant, en terme de probabilité: déterminer le handicap
c'est-à-dire le handicap qui rééquilibre la différence de niveau entre les deux joueurs, ou encore de telle sorte que
On peut résoudre numériquement ce problème, en calculant toutes les probabiltés
Il reste encore pour faire ces calculs à définir la probabilité
Estimation de la probabilité  de victoire d'un point
de victoire d'un point
Cette probabilité est finalement celle qui peut être la plus difficile à exprimer. Elle doit dépendre de l'écart entre les classements des deux joueurs et vérifier:
- à classement égal, pour un écart
 , on doit avoir
, on doit avoir 
- pour un écart "important", cette probabilité peut tendre vers 1
où
Cela correspond au choix fait dans cet article où une dépendance proportionnelle est trouvée entre les écarts de classements et la propabilité
Néanmoins, une probabilité de gain trop proche de 1 conduit à des points de handicap très élevés, la totalité des points de la rencontre moins 1 ou 2 points.
Dans l'article précédent, les auteurs préconisent de limiter le nombre de points de handicap (à 7 points au maximum sur 11, le contexte traîté étant celui du tennis de table).
On peut aussi atténuer les probabilités de gain d'un point, par exemple en prenant pour cette probabilité
Parties avec 2 points d'écart
Exemple d'une partie en  points
points
Une règle généralement utilisée consiste à imposer que le vainqueur ait au minimum deux points de plus que son adversaire.
À chaque situation d'égalité, la partie est relancée.
{$A_{1/0}$}
\rput[l](1.1,-1.5){$B_{0/1}$}
\psline(3,2)(2,1.5)(3,1)
\rput[l](3.1,2){\blue$A_{2/0}$}
\rput[l](3.1,1){\magenta\fbox{\black$B_{1/1}$}}
\psline(3,-2)(2,-1.5)(3,-1)
\rput[l](3.1,-1){\magenta\fbox{\black$A_{1/1}$}}
\rput[l](3.1,-2){\red$B_{0/2}$}
\psline(5,1.5)(4,1)(5,1)
\rput[l](5.1,1.5){$A_{2/1}$}
\psline(7,2)(6,1.5)(7,1.5)
\rput[l](7.1,2){\blue$A_{3/1}$}
\rput[l](7.1,1.5){\magenta\fbox{\black$B_{2/2}$}}
\rput[l](8.1,1.5){\dots}
\rput[l](5.1,1){$B_{1/2}$}
\psline(7,.5)(6,1)(7,1)
\rput[l](7.1,1){\magenta\fbox{\black$A_{2/2}$}}
\rput[l](8.1,1){\dots}
\rput[l](7.1,.5){\red$B_{1/3}$}
\psline(5,-1.5)(4,-1)(5,-1)
\rput[l](5.1,-1){$A_{2/1}$}
\rput[l](5.1,-1.5){$B_{1/2}$}
\psline(7,-2)(6,-1.5)(7,-1.5)
\rput[l](7.1,-2){\red$B_{1/3}$}
\rput[l](7.1,-1.5){\magenta\fbox{\black$A_{2/2}$}}
\rput[l](8.1,-1.5){\dots}
\psline(7,-.5)(6,-1)(7,-1)
\rput[l](7.1,-1){\magenta\fbox{\black$B_{2/2}$}}
\rput[l](8.1,-1){\dots}
\rput[l](7.1,-.5){\blue$A_{3/1}$}
\end{pspicture}\]](fich-IMG/76.png)
Le calcul de la probabilité de gain de la rencontre pour
En fait, on peut faire simplement le calcul en évitant un calcul de somme infinie en posant
Avec cette notation, on a ici la probabilité de victoire pour
Il reste à déterminer
ce qui nous permet d'obtenir directement, en isolant
![\[P_{eq}=\dfrac{p^2}{1-2pq}\]](fich-IMG/86.png)
En résumé, la probabilité de gain pour
![\[P_2=p^2+\dfrac{2p^3q}{1-2pq}\]](fich-IMG/88.png)
Partie en  points
points
On peut rapidement généraliser le résultat précédent. Sans deux points d'écart, on avait:
![\[P_N=\dsp\sum_{i=0}^{N-1}\lp\bgar{c}N+i-1\\i\enar\rp p^Nq^i\]](fich-IMG/90.png)
Dans cette expression, pour
![\[P_N=\dsp\sum_{i=0}^{N-2}\lp\bgar{c}N+i-1\\i\enar\rp p^Nq^i
+\lp\bgar{c}2N-2\\N-1\enar\rp p^{N-1}q^{N-1} P_{eq}\]](fich-IMG/92.png)
et donc, avec l'expression de
![\[P_N=\dsp\sum_{i=0}^{N-2}\lp\bgar{c}N+i-1\\i\enar\rp p^Nq^i
+\lp\bgar{c}2N-2\\N-1\enar\rp \dfrac{p^{N+1}q^{N-1}}{1-2pq}\]](fich-IMG/94.png)
Partie en  points avec
points avec  points de handicap
points de handicap
Si on attribue initialement
![\[P_N=\dsp\sum_{i=0}^{N-2-H}\lp\bgar{c}N+i-1\\i\enar\rp p^Nq^i
+\lp\bgar{c}2N-2-H\\N-1-H\enar\rp \dfrac{p^{N+1}q^{N-1-H}}{1-2pq}\]](fich-IMG/99.png)