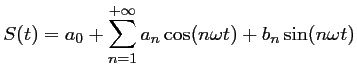
où la pulsation
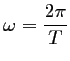 .
.
Déterminer la décomposition de la fonction ![]() en série de Fourier
revient à déterminer les coefficients
en série de Fourier
revient à déterminer les coefficients
![]() (valeur moyenne de
(valeur moyenne de ![]() ), et pour
), et pour
![]() ,
,
![]() et
et
![]() ,
donnés par:
,
donnés par:
![\begin{displaymath}\begin{array}{ll}
a_0
&\displaystyle =\dfrac{1}{T}\int_{\alp...
...ha+T} f(t)\sin\left(n\omega T\right)\,dt \\ [0.4cm]
\end{array}\end{displaymath}](img10.png)
pour un réel
![$\displaystyle f(t)=
\left\{\begin{array}{lll}
1 &\text{ si } & 0\leqslant t<\pi \\ [0.4cm]
-1 &\text{ si } & \pi\leqslant t<2\pi
\end{array}\right.
$](img14.png)

Calcul des coefficients de la série de Fourier:
La période de
![]() est
est
![]() , soit une pulsation
, soit une pulsation
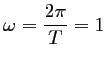 .
.
La valeur moyenne de
![]() est:
est:
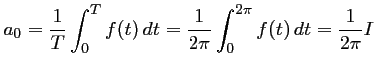
Comme la fonction est définie par morceaux sur
![\begin{displaymath}\begin{array}{lcll}
I
&=&\displaystyle \int_0^{\pi} f(t)\,dt ...
... - 0 \Bigr] &- \Bigl[ 2\pi - \pi\ \Bigr]
=\pi-\pi=0
\end{array}\end{displaymath}](img21.png)
Ainsi,
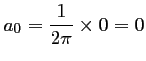 .
.
Remarque:
La fonction
![]() étant impaire, on a directement
étant impaire, on a directement
![]() ,
résultat que l'on retrouve ici...
,
résultat que l'on retrouve ici...
Pour les autres coefficients:
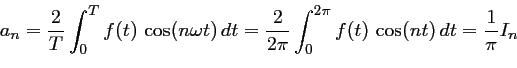
On procède de la même façon pour calculer ![]() :
:
![\begin{displaymath}\begin{array}{lccl}
I_n
&=&\displaystyle \int_0^{2\pi} f(t)\,...
...{1}{n}\Bigl[ \sin(2n\pi)-\sin(n\pi)\Bigr]\\ [0.4cm]
\end{array}\end{displaymath}](img26.png)
or, pour tout entier
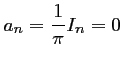
Remarque:
La fonction
![]() étant impaire, on a aussi directement
étant impaire, on a aussi directement
![]() ,
résultat que l'on retrouve aussi ici...
,
résultat que l'on retrouve aussi ici...
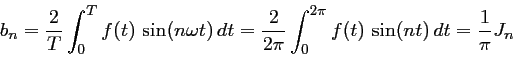
On procède de la même façon pour calculer ![]() :
:
![\begin{displaymath}\begin{array}{lccl}
J_n
&=&\displaystyle \int_0^{2\pi} f(t)\,...
...{1}{n}\Bigl[ \cos(2n\pi)-\cos(n\pi)\Bigr]\\ [0.4cm]
\end{array}\end{displaymath}](img33.png)
or, pour tout entier
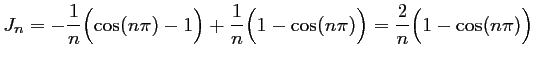
et donc
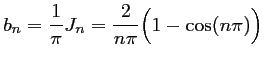
La série de Fourier associée à la fonction
![]() s'écrit ainsi:
s'écrit ainsi:

(voir le cours et l'expression des coefficients de Fourier pour une fonction paire ou impaire; attention, ces expressions ne sont pas dans le formulaire du BTS).
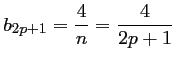 .
.
La série de Fourier s'écrit alors:
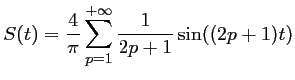
Le calcul des coefficients de Fourier d'une fonction quelconque
![]() se ramène généralement (du moins pour le programme du BTS) aux
calculs suivants (à des coefficients multiplicatifs près):
se ramène généralement (du moins pour le programme du BTS) aux
calculs suivants (à des coefficients multiplicatifs près):
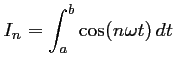 et,
et,
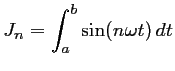
et
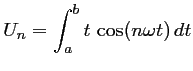 et,
et,
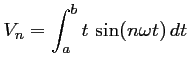
ainsi que (plus rarement, mais à savoir calculer néanmoins)
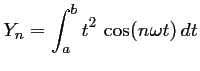 et,
et,
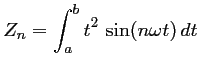
Bien évidemment, ces calculs ne sont pas à connaître
par c
![]() ur,
par contre il faut savoir les effectuer sans hésiter!
ur,
par contre il faut savoir les effectuer sans hésiter!
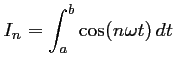 et,
et,
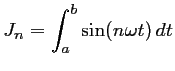
Ces calculs ont déjà été effectués lors des calculs des coefficients de Fourier du
On connaît ici directement des primitives de
![]() et
et
![]() :
:
![$\displaystyle I_n=\int_a^b \cos(n\omega t)\,dt
=\Bigl[ \dfrac{1}{n\omega} \sin...
...t)\Bigr]_a^b
=\dfrac{1}{n\omega}\Bigl[ \sin(n\omega b) - \sin(n\omega a)\Bigr]
$](img51.png)
![$\displaystyle I_n=\int_a^b \sin(n\omega t)\,dt
=\Bigl[ -\dfrac{1}{n\omega} \co...
...)\Bigr]_a^b
=-\dfrac{1}{n\omega}\Bigl[ \cos(n\omega b) - \cos(n\omega a)\Bigr]
$](img52.png)
Calculer, pour tout entier
![]() ,
,
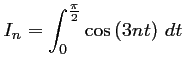 et
et
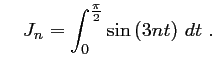
Correction:
Une primitive de
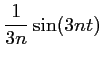 ,
et donc ,
et donc
![$\displaystyle I_n
=\Bigl[\ \dfrac{1}{3n}\sin(3nt)\ \Bigr]_0^{\frac{\pi}{2}}
=\d...
...\pi}{2}\right)-\sin(0)\right)
=\dfrac{1}{3n} \sin\left(3n\dfrac{\pi}{2}\right)
$](img57.png) De même, une primitive de 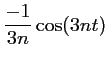 ,
et donc ,
et donc
![$\displaystyle J_n
=\Bigl[\ \dfrac{-1}{3n}\cos(3nt)\ \Bigr]_0^{\frac{\pi}{2}}
=\...
...\cos(0)\right)
=\dfrac{-1}{3n}\left(\cos\left(3n\dfrac{\pi}{2}\right)-1\right)
$](img61.png) |
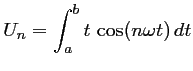 et,
et,
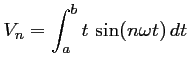
On peut ici (et doit...) utiliser une intégration par parties, dont on rappelle la formule générale:
![$\displaystyle \int_a^b u\,v' = \Bigl[\ u\,v\ \Bigr]_a^b - \int_a^b u'\,v
$](img65.png)
L'idée est de dériver le "
![]() " dans les intégrales
" dans les intégrales
![]() et
et
![]() afin de se retrouver avec des intégrales plus simples du type de
afin de se retrouver avec des intégrales plus simples du type de
![]() et
et
![]() .
.
On intègre donc par parties
![]() :
:
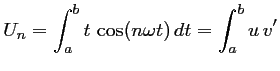
avec
![$ \left\{\begin{array}{ll}
u(t)=t \\ [0.4cm]
v'(t)=\cos(n\omega t)
\end{array}\right.$](img68.png) soit,
soit,
![$ \left\{\begin{array}{ll}
u'(t)=1 \\ [0.4cm]
v(t)=\dfrac{1}{n\omega}\sin(n\omega t)
\end{array}\right.$](img69.png)
et ainsi,
![\begin{displaymath}\begin{array}{ll}
\displaystyle U_n
&\displaystyle =\int_a^b ...
...1}{n\omega} \int_a^b \sin(n\omega t)\,dt \\ [0.4cm]
\end{array}\end{displaymath}](img70.png)
et il n'y a plus qu'à calculer la dernière intégrale qui n'est autre que
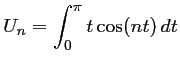 .
.
Correction:
On intègre ![$ \left\{\begin{array}{ll}
u(t)=t \\ [0.4cm]
v'(t)=\cos(nt)
\end{array}\right.$](img72.png) soit,
soit,
![$ \left\{\begin{array}{ll}
u'(t)=1 \\ [0.4cm]
v(t)=\dfrac{1}{n}\sin(nt)
\end{array}\right.$](img73.png)
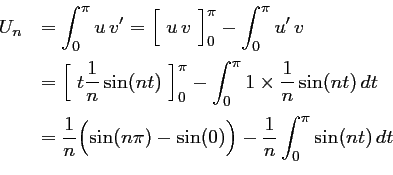
or, 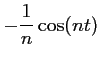 ,
d'où,
,
d'où,
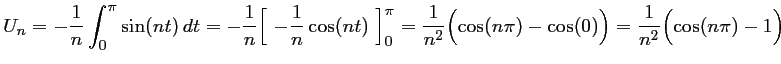
car
|
De même pour
![]() ,
on intègre donc par parties:
,
on intègre donc par parties:
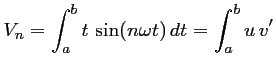
avec
![$ \left\{\begin{array}{ll}
u(t)=t \\ [0.4cm]
v'(t)=\sin(n\omega t)
\end{array}\right.$](img84.png) soit,
soit,
![$ \left\{\begin{array}{ll}
u'(t)=1 \\ [0.4cm]
v(t)=\dfrac{{\bf\textcolor{red}{-}}1}{n\omega}\cos(n\omega t)
\end{array}\right.$](img85.png) et ainsi,
et ainsi,
![\begin{displaymath}\begin{array}{ll}
\displaystyle U_n
&\displaystyle =\int_a^b ...
...1}{n\omega} \int_a^b \cos(n\omega t)\,dt \\ [0.4cm]
\end{array}\end{displaymath}](img86.png)
et il n'y a plus qu'à calculer la dernière intégrale qui n'est autre que
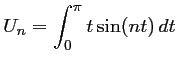 .
.
Correction:
On intègre
![$ \left\{\begin{array}{ll}
u(t)=t \\ [0.4cm]
v'(t)=\sin(nt)
\end{array}\right.$](img88.png) soit,
soit,
![$ \left\{\begin{array}{ll}
u'(t)=1 \\ [0.4cm]
v(t)=-\dfrac{1}{n}\cos(nt)
\end{array}\right.$](img89.png)
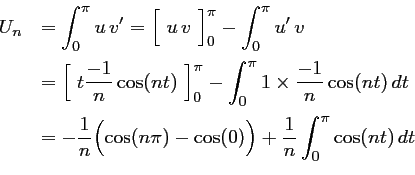
or, 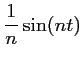 ,
d'où,
,
d'où,
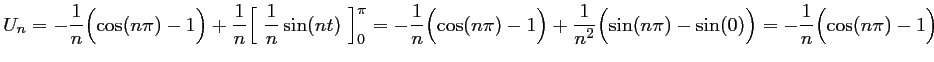
car |
Pour le calcul de
![]() et
et
![]() ,
,
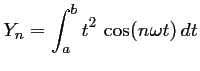 et,
et,
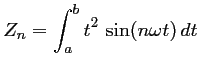
on utilise une double intégration par parties (c'est-à-dire deux intégrations par parties successives, l'une après l'autre):
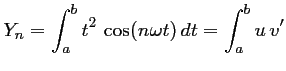
avec
![$ \left\{\begin{array}{ll}
u(t)=t^2 \\ [0.4cm]
v'(t)=\cos(n\omega t)
\end{array}\right.$](img97.png) soit,
soit,
![$ \left\{\begin{array}{ll}
u'(t)=2t \\ [0.4cm]
v(t)=\dfrac{1}{n\omega}\sin(n\omega t)
\end{array}\right.$](img98.png)
et ainsi,

et il ne reste plus qu'à calculer la dernière intégrale qui n'est autre que
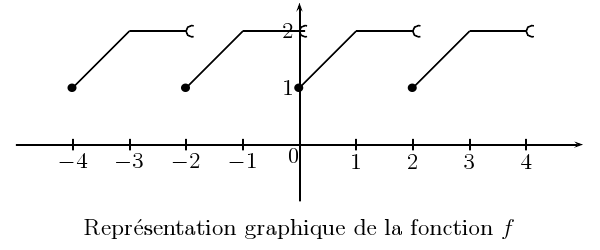
Soit la fonction
![]() , périodique de période 2, définie par
, périodique de période 2, définie par
![\begin{displaymath}
f(t)=\left\{
\begin{array}{lll}
t+1 & \text{ si } & 0\leqsla...
...\ [0.4cm]
2 & \text{ si } & 1\leqslant t <2
\end{array}\right.\end{displaymath}](img101.png)
La valeur moyenne de ![]() est:
est:
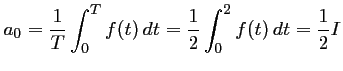
avec,
![\begin{displaymath}\begin{array}{llll}
I
&=&\displaystyle \int_0^2 f(t)\,dt \\ [...
...isplaystyle +2\Bigr[ 1\Bigl] \\ [0.4cm]
&=&\dfrac72
\end{array}\end{displaymath}](img104.png)
ainsi,
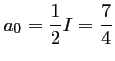 .
.
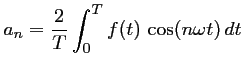
avec la période
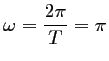 ,
,
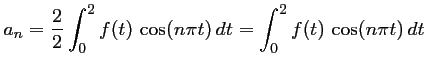
On décompose l'intégrale en utilisant la définition par morceaux de
![\begin{displaymath}\begin{array}{llcl}
a_n
&=&\displaystyle \int_0^1 f(t)\,\cos(...
...splaystyle A_n
&\displaystyle + \ 2\ B_n \\ [0.4cm]
\end{array}\end{displaymath}](img110.png)
L'intégrale
![]() se calcule en utilisant une intégration par parties
(cf. calcul de l'intégrale
se calcule en utilisant une intégration par parties
(cf. calcul de l'intégrale
![]() ), tandis que
), tandis que
![]() s'intègre
directement en utilisant une primitive de
s'intègre
directement en utilisant une primitive de
![]() (cf. calcul de l'intégrale
(cf. calcul de l'intégrale ![]() ):
):
![\begin{displaymath}\begin{array}{llll}
A_n
&=&\displaystyle \Bigl[ (t+1)\dfrac{1...
...rac{1}{n^2\pi^2}\Bigl[ \cos(2n\pi)-\cos(n\pi)\Bigr]
\end{array}\end{displaymath}](img114.png)
or, pour tout entier
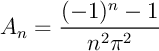 .
.
![\begin{displaymath}\begin{array}{llll}
B_n
&=&\displaystyle \int_1^2\cos(n\pi t)...
...dfrac{1}{n\pi}\Bigl[ \sin(2n\pi)-\sin(n\pi)\Bigr]=0
\end{array}\end{displaymath}](img117.png)
car, pour tout entier
Au final,
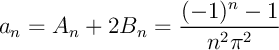
De même que pour les coefficients
![]() ,
,
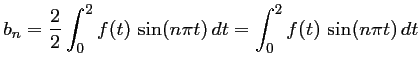
On décompose l'intégrale en utilisant la définition par morceaux de
![\begin{displaymath}\begin{array}{llcl}
b_n
&=&\displaystyle \int_0^1 f(t)\,\sin(...
...splaystyle C_n
&\displaystyle + \ 2\ D_n \\ [0.4cm]
\end{array}\end{displaymath}](img121.png)
L'intégrale
![]() se calcule en utilisant une intégration par parties
(cf. calcul de l'intégrale
se calcule en utilisant une intégration par parties
(cf. calcul de l'intégrale
![]() ), tandis que
), tandis que
![]() s'intègre
directement en utilisant une primitive de
s'intègre
directement en utilisant une primitive de
![]() (cf. calcul de l'intégrale
(cf. calcul de l'intégrale
![]() ):
):
![\begin{displaymath}\begin{array}{llll}
C_n
&=&\displaystyle \Bigl[ (t+1)\dfrac{-...
...rac{1}{n^2\pi^2}\Bigl[ \sin(2n\pi)-\sin(n\pi)\Bigr]
\end{array}\end{displaymath}](img125.png)
or, pour tout entier
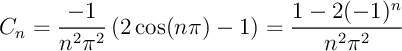 .
.
![\begin{displaymath}\begin{array}{llll}
D_n
&=&\displaystyle \int_1^2\sin(n\pi t)...
...i)\Bigr]
=\dfrac{-1}{n\pi}\Bigl[ 1-\cos(n\pi)\Bigr]
\end{array}\end{displaymath}](img127.png)
.
Au final,
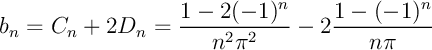
Soit la fonction
![]() ,
,
![]() -périodique, définie par
-périodique, définie par
![$ f(t)=
\left\{\begin{array}{lll}
t & \text{si} & 0\leqslant t \leqslant \dfrac{...
...\\ [0.4cm]
\dfrac{\pi}{2} & \text{si} & \dfrac{\pi}{2}<t<\pi
\end{array}\right.$](img130.png)
|
On représente d'abord
|
La période de
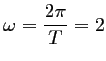 .
.
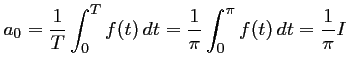
avec 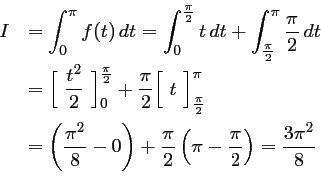
Ainsi, 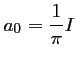 ,
soit
,
soit
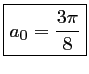 .
.
|
Pour tout entier
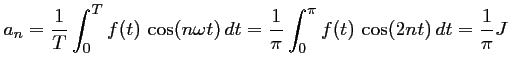
avec, 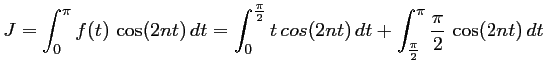
La première intégrale se calcule en utilisant une intégration par parties: ![\begin{displaymath}\begin{array}{ll}
\displaystyle \int_0^{\frac{\pi}{2}} t\,co...
...dfrac{1}{4n^2}\Bigl[ \cos(2n\pi)-\cos(n\pi)\Bigr]
\end{array} \end{displaymath}](img143.png)
or, pour tout entier
et ainsi,
Par ailleurs, ![$\displaystyle \int_{\frac{\pi}{2}}^\pi \dfrac{\pi}{2}\,\cos(2nt)\,dt
=\dfrac{\...
...r]_{\frac{\pi}{2}}^\pi
=\dfrac{\pi}{4n}\Bigl[\sin(2n\pi)-\sin(n\pi\Bigr]
=0
$](img146.png)
car, pour tout entier
|
De même que précédemment,
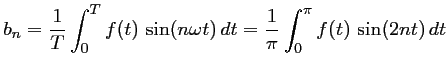
avec, 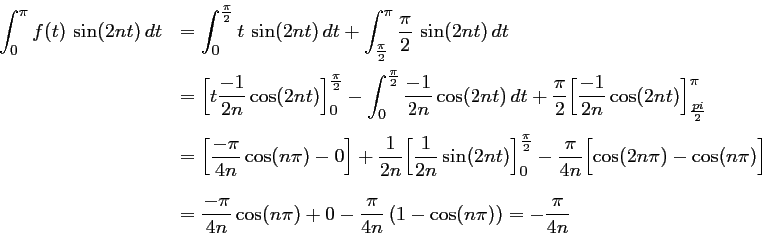
car,
Au final,
|
La valeur efficace
![\begin{displaymath}\begin{array}{ll}
\mu^2
&\displaystyle =\dfrac{1}{T}\int_0^...
...pi-\dfrac{\pi}{2}\Bigr]\right)
=\dfrac{\pi^2}{24}
\end{array}\end{displaymath}](img154.png)
Ainsi, la valeur efficace de 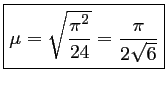 .
.
|


