Système d'équations cartésiennes d'une droite passant par deux points
Dans l'espace muni d'un repère orthonormé
,
on considère les points
et 
.
Établir un système d'équations cartésiennes de la droite
.
,
on considère les points
et .
Établir un système d'équations cartésiennes de la droite
.
Correction
est un vecteur directeur de 
dont une représentation paraméétrique est donc,
avec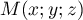 
,
![\[\overrightarrow{AM}=t\overrightarrow{AB}\iff
\la\begin{array}{ll}
x=-1+3t \\
y=2-3t\\
z=3+t
\enar\right.\!\!\!,t\in\R\]](/Generateur-Devoirs/Colles/Geom3D/ex5_c/4.png)
En changeant de paramètre
, on a
![\[\begin{array}{ll}&\la\begin{array}{ll}x=-1+3(z-3) \\
y=2-3(z-3)\enar\right.\\[2em]
\iff&\la\begin{array}{ll}x-3z+10=0 \\
y+3z-11=0\enar\right.\enar\]](/Generateur-Devoirs/Colles/Geom3D/ex5_c/6.png)
qui est un système d'équations cartésiennes de la droite
.
Cacher la correction
est un vecteur directeur de dont une représentation paraméétrique est donc,
avec ,
En changeant de paramètre
, on a
qui est un système d'équations cartésiennes de la droite
.
Cacher la correction
Tag:Géométrie dans l'espace
Autres sujets au hasard:
